Linear Independence and the Wronskian
Recall from linear algebra that two vectors v and w are called linearly
dependent if there are nonzero constants c1
and c2 with.
c1v
+ c2w = 0
We can think of differentiable functions f(t)
and g(t) as being vectors in the vector space of differentiable
functions. The analogous definition is
Let f(t)
and g(t) be
differentiable functions. Then they are called linearly
dependent if there are nonzero constants
c1 and c2
with
c1f(t)
+ c2g(t) = 0
for all t.
Otherwise they are called linearly independent.
Example
The functions f(t) = 2sin2 t
and g(t) = 1 - cos2(t)
are linearly dependent since
(1)(2sin2
t) + (-2)(1 - cos2(t)) = 0
Example
The functions f(t) = t and g(t)
= t2 are linearly independent since otherwise there
would be nonzero constants c1 and c2
such that
c1t
+ c2t2 = 0
for all t. First let t
= 1. Then
c1
+ c2 = 0
Now let t = 2. Then
2c1
+ 4c2 = 0
This is a system of 2 equations and two unknowns. The determinant of
the corresponding matrix is
4 - 2
= 2
Since the determinant is nonzero, the only solution is the trivial
solution. That is
c1
= c2 = 0
The two functions are linearly independent.
In the above example, we arbitrarily selected two values for t. It
turns out that there is a systematic way to check for linear dependence.
The following theorem states this way.
|
Theorem
Let f
and g
be differentiable on [a,b]. If
Wronskian W(f,g)(t0)
is
nonzero for some t0
in [a,b]
then f and
g
are linearly independent on [a,b].
If f
and g are linearly dependent then the
Wronskian is zero for all t in
[a,b].
|
Example
Show that the functions f(t) = t
and g(t) = e2t are linearly
independent.
Solution
We compute the Wronskian.
f '(t) =
1 g '(t) = 2e2t
The Wronskian is
(t)(2e2t) - (e2t)(1)
Now plug in 0 to get
W(f,g)(0) = -1
which is nonzero. We can conclude that f and
g are linearly
independent.
Proof
If
c1f(t)
+ c2g(t) = 0
Then we can take derivatives of both sides to get
c1f
'(t) + c2g '(t) = 0
This is a system of two equations with two unknowns. The determinant of
the corresponding matrix is the Wronskian. Hence, if the Wronskian is
nonzero at some t0, only the trivial solution exists. Hence
they are linearly independent.
There is a fascinating relationship between second order linear differential
equations and the Wronskian. This relationship is stated below.
|
Abel's Theorem
Let y1 and y2
be solutions on the differential equation
L(y) = y'' + p(t)y' + q(t)y = 0
where p and q
are continuous on [a,b]. Then the
Wronskian is given by
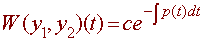
where c is a constant depending on only y1
and y2, but not on t.
The Wronskian is either zero for all t in [a,b]
or no t in [a,b]. |
Proof
First the Wronskian
W = y1y2' - y1'y2
has derivative
W'
= y1'y2' + y1y2'' - y1''y2
- y1'y2' = y1y2''
- y1''y2
Since y1 and y2
are solutions to the differential equation, we have
y1''
+ p(t)y1' + q(t)y1 = 0
y2''
+ p(t)y2' + q(t)y2 = 0
Multiplying the first equation by -y2 and
the second by y1 and adding gives
(y1y2''
- y1''y2) + p(t)(y1y2' - y1'y2)
= 0
This can be written as
W' + p(t)W
= 0
This is a separable differential equation with
dW/W
= -p(t)dt
Now integrate and Abel's theorem appears.
Example
Find the Wronskian (up to a constant) of the differential equations
y'' + cos(t) y' = 0
Solution
We just use Abel's theorem, the integral of cos t is
sin t hence the Wronskian is
W(t)
= ce-sin t
A corollary of Abel's theorem is the following
Corollary
Let y1
and y2 be
solutions to the differential equation
L(y)
= y'' + p(t)y' + q(t)y = 0
Then either W(y1,y2)
is zero for all t or never zero.
Example
Prove that
y1(t)
= 1 - t and y2(t)
= t3
cannot both be solutions to a differential equation
y'' + p(t)y
+ q(t) = 0
for p(t) and q(t)
continuous on [-1,5].
Solution
We compute the Wronskian
y1'
= -1 y2'
= 3t2
W(y1,y2)
= (1 - t)(3t2) - (t3)(-1) = 3t2
- 2t3
Notice that the Wronskian is zero at t = 0
but nonzero at t = 1. By the
above corollary, y1 and y2
cannot both be solutions.
Back
to the Linear Second Order Differential Equations Home Page
Back
to the Differential Equations Home Page
Back to the Math
Department Home Page
e-mail Questions and Suggestions
![]()