Uniqueness and Existence for Second Order Differential Equations

Recall that for a first order linear differential equation

        y' + p(t)y  =  g(t)        y(t₀)  =  y₀

if p(t) and g(t) are continuous on [a,b], then there exists a unique solution on the interval [a,b].

We can ask the same questions of second order linear differential equations.  We need to first make a few comments.  The first is that for a second order differential equation, it is not enough to state the initial position.  We must also have the initial velocity.  One way of convincing yourself, is that since we need to reverse two derivatives, two constants of integration will be introduced, hence two pieces of information must be found to determine the constants.  

A second comment is that of notation.  Let 

        y'' + p(t)y' + q(t)y  =  g(t)   

be a second order linear differential equation.  Then we call the operator 

        L(y)  =  y'' + p(t)y' + q(t)y

the corresponding linear operator.  Thus we want to find solutions to the equation

        L(y)  =  g(t)        y(t₀)  =  y₀     y'(t₀)  =  y'₀

We will state the following theorem without proof.  The proof is well above the level of this course.

Example

Find the largest interval where 

        (t² - 1)y'' + 3ty' + cos t y  =  e^t       y(0)  =  4, y'(0)  =  5

is guaranteed to have a unique solution.

Solution

We first put it into standard form

        y'' + 3t/(t² - 1)y' + (cos t)/(t² - 1) y  =  e^t /(t² - 1)       y(0)  =  4, y'(0)  =  5

p, q, and g are all continuous except at t  =  -1  and t  =  1.  The theorem tells us that there is a unique solution on [-1,1].

Homogeneous Linear Second Order Differential Equations

Next we will investigate solutions to homogeneous differential equations.  Consider the homogeneous linear differential equation 

        L(y)  =  0

We have the following theorem

Using the terminology of linear algebra, we know that L is a linear transformation of the vector space of differentiable functions into itself.  The theorem reminds us that the kernel of a linear transformation is a vector subspace.

Proof

        L(c₁y₁ + c₂y₂)  =  (c₁y₁ + c₂y₂)'' + p(t)(c₁y₁ + c₂y₂)' + q(t)(c₁y₁ + c₂y₂)

        =  c₁y₁'' + c₂y₂'' + p(t)c₁y₁' + p(t)c₂y₂' + q(t)c₁y₁ + q(t)c₂y₂

        =  c₁y₁'' + p(t)c₁y₁' + q(t)c₁y₁ + q(t)c₂y₂'' +  p(t)c₂y₂' + q(t)c₂y₂ 

        =  c₁(y₁'' + p(t)y₁' + q(t)y₁) + c₂(y₂'' + p(t)y₂' + q(t)y₂)

        =  c₁L(y₁) + c₂L(y₂)  =  0 + 0  =  0.

Next, we investigate the initial conditions.  If we find a general solution to the homogenous system, can we choose constants such that the solution satisfies the initial conditions?  That is can we find c₁ and c₂ such that 

        c₁y₁(t₀) + c₂y₂(t₀)  =  y₀

        c₁y₁'(t₀) + c₂y₂'(t₀)  =  y₀'

  We can put this into a matrix equation

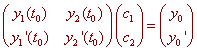
This has a unique solution if and only if the determinant of the matrix is not zero.  This determinant is called the Wronskian.

This proves the following theorem

Example

Consider the differential equation 

        y'' + 2y' - 8y  =  0

It is easy to check that the general solution is given by 

        y  =  c₁e^2t + c₂e^-4t 

The Wronskian of 

        y₁  =  e^2t     y₂  =  e^-4t 

is given by 

        e^2t(-4e^-4t) - (2e^2t)e^-4t  =  -4e^-2t - 2e^-2t  =  -6e^-2t

Which is never zero.  We can conclude that any initial value problem will have a unique solution of the form 

        y  =  c₁e^2t + c₂e^-4t 

Back to the Linear Second Order Differential Equations Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions