General Linear Transformations
We have seen that a linear transformation L from Rn to Rm is a function with domain Rn, range a subset of Rm satisfying
1) L(u + v) = L(u) + L(v) 2) L(cu) = cL(u)
for any vectors u and v and scalar c.
We can use the analogous definition for a linear transformation of vector spaces.
Definition
Let V and W be vector spaces. Then a linear transformation from V to W is a function with domain V and range a subset of W satisfying
1) L(u + v) = L(u) + L(v) 2) L(cu) = cL(u)
for any vectors u and v in V and scalar c.
Examples
Example
Let V be the vector space of (infinitely) differentiable functions and define D to be the function from V to V given by
D(f(t)) = f '(t)
Then D is a linear transformation since
D(f(t) + g(t)) = (f(t) + g(t))' = f '(t) + g'(t) = D(f(t)) + D(g(t))
and
D(cf(t)) = (cf(t))' = c f '(t) = cD(f(t))
Example
Let V be the space of continuous functions and define I to be the function from V to V given by
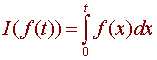
Then I is a linear transformation. (Check this)
Example
Let V be M2x2 and W be P3 then define L to be the function from V to W with
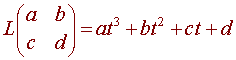
Then L is a linear transformation since
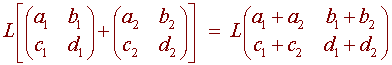
= (a1 + a2)t3 + (b1 + b2)t2 + (c1 + c2)t + (d1 + d2)
= a1t3 + b1t2 + c1t + d1 + a2t3 + b2t2 + c2t + d2
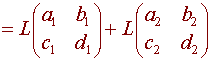
and
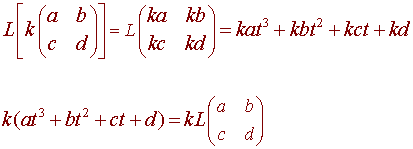
Example
Let V = P2 and let W be the real numbers. Show that the function L from V to W defined by
L(at2 + bt + c) = abc
is not a linear transformation.
Solution
We can pick just about any example and show that either the first or second property does not hold. For example, let
v = 2t2 + 3t + 4 and c = 5
then
L(cv) = L(10t2 + 15t + 20) = (10)(15)(20) = 3000
and
cL(v) = 5L(2t2 + 3t + 4) = 5(2)(3)(4) = 120
since these are not equal, L is not a linear transformation.
When we looked at linear transformations from Rn to Rm, we stated and proved several properties. A close look at these proofs will show that they only used the properties of vector spaces and linearity. We now state the properties. For each of the theorems below, assume that L is a linear transformation from a vector space V to a vector space W, and u, v, v1, v2, ... ,vn are vectors in V.
Theorem
1. L(0) = 0
2. L(u - v) = L(u) - L(v)
3. L(c1v1 + c2v2 + ... + cnvn) = c1L(v1) + c2L(v2) + ... + cnL(vn)
We will prove statement 3 and leave the rest for you. We prove the statement by induction.
For n = 1, the statement is just property 2 of a linear transformation.
L(c1v1) = c1L(v1)
Now assume that the statement is true for n = k. Then
L(c1v1 + c2v2 + ... + ckvk) = c1L(v1) + c2L(v2) + ... + ckL(vk)
We have
L(c1v1 + c2v2 + ... + ckvk + ck+1vk+1)
= L((c1v1 + c2v2 + ... + ckvk) + ck+1vk+1)
= L(c1v1 + c2v2 + ... + ckvk) + L(ck+1vk+1)
= c1L(v1) + c2L(v2) + ... + ckL(vk) + ck+1L(vk+1)
So by mathematical induction the theorem is true.
We have seen that general linear transformations behave the same as linear transformation from Rn to Rm. The next theorem solidifies this fact.
Theorem
Let S = {v1, v2, ... ,vn} be a basis for V. And let L be a linear transformation from V to a vector space W. Then L is completely determined by the image of the basis S.
This means that if we know L(, L(v2), ... ,L(vn) then we know L(v) for any vector v.
Proof
If v is a vector in V, then since S is a basis, we can write
v = c1v1 + c2v2 + ... + ckvk
so that
L(v) = L(c1v1 + c2v2 + ... + ckvk)
= c1L(v1) + c2L(v2) + ... + ckL(vk)
Example
Let L be the linear transformation from P1 to M2x2 such that
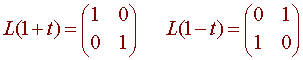
Find L(3 + t).
Solution
We need to find the coordinates of v = 3 + t with respect to the basis S = {1 + t, 1 - t}. We have
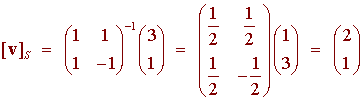
so that
v = 2(1 + t) + 1(1 - t)
and
L(v) = L(2(1 + t) + 1(1 - t)) = 2L(1 + t) + L(1 - t)
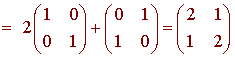
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions