Linear Transformations on Rⁿ

Definition of a Linear Transformation

In your travels throughout your mathematical career there has been one theme that persists in every course.  That theme is functions.  Recall that a function is a rule that assigns every element from a domain set to a unique element of a range set.  If the domain and range are both the real numbers, then a function is the familiar real valued function.  If the domain is a real number and the range is Rⁿ then the function is a vector valued function or a parametrically defined curve.  If the domain is Rⁿ and the range is the real numbers, then the function is a function of several variables.  In linear algebra we are interested in special functions where the domain is Rⁿ and the range is R^m. 

Definition

Let

        L:  Rⁿ  --->  R^m

be a function such that the following two properties hold:

1. L(u + v)  =  L(u) + L(v)
   
   
2. L(cu)  =  cL(u)

Then the function is called a linear transformation.

This definition calls for some examples. 

Example

Let

        L:  R²  --->  R³

be defined by

        L(x,y)  =  (y, x, x + y)

Show that L is a linear transformation.

Solution

First, we prove the first property.  Suppose that

        u  =  (u₁,u₂)        and       v  =  (v₁,v₂)

then

        L(u + v)  =  L(u₁ + v₁, u₂ + v₂)

        =  (u₂ + v₂, u₁ + v₁, u₁ + v₁ + u₂ + v₂)

and

        L(u) + L(v)  =  (u₂, u₁, u₁ + u₂) + (v₂, v₁, v₁ + v₂)

         =  (u₂ + v₂, u₁ + v₁, u₁ + u₂ +v₁ + v₂)

Hence

        L(u + v)  =  L(u) + L(v)

Now for the second property.  We have

        L(cu)  =  L(c(u₁, u₂))  =  L(cu₁, cu₂) 

        =  (cu₂, cu₁, cu₁ + cu₂)  =  c(u₂, u₁, u₁ + u₂)  =  cL(u)

Since properties 1 and 2 hold, we can conclude that L is a linear transformation.

Example

Show that the function

        f:  R³ --->  R²

defined by

        f(x, y, z)  =  (xy, yz)

is not a linear transformation

Solution

To show a function is not a linear transformation, we just need to find an example that demonstrates the failure of one of the properties.  We have

        f(2(3, 4, 5))  =  f(6, 8, 10)  =  (48, 80)

and

        2(f(3, 4, 5))  =  2(12, 20)  =  (24, 40)

since these are not equal, we can conclude that f is not a linear transformation.

It is a simple consequence to the two properties that if L is a linear transformation then

        L(c₁v₁ + c₂v₂ + ... + c_kv_k)  =  c₁L(v₁) + c₂L(v₂) + ... + c_kL(v_k)

or in sigma notation

        L(Sc_iv_i)  =  S L(c_iv_i)

The Matrix of a Linear Transformation

Example/Theorem

Let A be an m x n matrix and let

        L:  Rⁿ  --->  R^m

be defined by

        L(u)  =  Au^T

Then L is a linear transformation.

Proof

The proof is just a matter of stating the corresponding properties of matrices. We have

        L(u + v)  =  A(u + v)^T  =  A(u^T + v^T)  

                       =  Au^T + Av^T  =  L(u) + L(v)

and 

        L(cu)  =  A(cu)^T  =  A(cu^T)  

                   =  cAu^T  =  cL(u)

The converse is also true.

Theorem

Let 

        L:  R^m  --->  Rⁿ 

be a linear transformation.  Then there is a unique matrix A such that 

        L(u)  =  Au^T

Proof

Recall that the vector e_i is the vector with i^th component equal to 1 and all others zero.  Any vector 

        v  =  (v₁,v₂, ... ,v_m)  =  v₁e₁ + v₂e₂ + ... + v_me_m 

We let the i^th column of A be the vector

        L(e_i)

Notice that 

        Ae_i  =  the i^th column of A 

so that

        L(e_i)  =  Ae_i 

Then 

        L(v)  =  L(v₁, v₂, ... , v_m)  =  L(v₁e₁ + v₂e₂ + ... + v_me_m)  

        =   v₁L(e₁) + v₂L(e₂) + ... + v_mL(e_m)  =  v₁Ae₁ + v₂Ae₂ + ... + v_mAe_m 

        =  A(v₁e₁ + v₂e₂ + ... + v_me_m)  =   Av^T 

To show that the matrix is unique, we just notice that if B is a matrix with 

        L(v)  =  Bv^T

then 

        Be_i  =  L(e_i)  =  Ae_i 

so that the columns of A and B are the same.

Example

For the linear transformation from the first example,

        L(x, y)  =  (y, x, x + y)

We have

        L(1, 0)  =  (0, 1, 1)        L(0, 1)  =  (1, 0, 1)

so that the matrix A that represents the linear transformation is

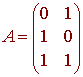
Properties of Linear Transformations

There are a few notable properties of linear transformation that are especially useful.  They are the following.

1. L(0)  =  0
   
   
2. L(u - v)  =  L(u) - L(v)

Notice that in the first property, the 0's on the left and right hand side are different.  The left hand 0 is the zero vector in R^m and the right hand 0 is the zero vector in Rⁿ.  The proofs of these can be done in two ways.  One way is to use the definition of a linear transformation.  A quicker way is to note that a linear transformation can be represented as a matrix.  These two properties are just properties of matrices.

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions