Name
MAT 154A Practice Exam 3
Please work out each of the given
problems. Credit will be based on
the steps that you show towards the final answer.
Do all your work and give all your answers on you own sheet of paper.
Show your work.
Problem 1
Sketch the graphs of the given functions:
A.
x2
+ 4y2 = 1
9
B.
x2 + y2 + 2x - 4y
- 4 = 0
A. Find the first four terms of the sequence whose general term is given. Then find the 100th term.
an = n - 1/n
B. Expand and simplify
![]()
C. (8 Points) Write the series in summation notation
1 2
3 4
+ +
+ + ...
2
3
4
5
Problem
3
A) Find the indicated unknown
8, 13, 18, 23, ..., 88 n = ?
B) Find the sum of the given series
![]()
Problem
4
A. Find the indicated unknown
a1 = 5, a5 = 0.008 r = ?
B. A rubber ball is dropped on a hard surface and bounces to a height of 200 ft. On each rebound it bounces 95% as high as on the previous bounce. How high does the ball bounce on the 20th bounce?
Problem
5
A. Find the sum of the infinite series if it exists.
1
1
1
1+
+ +
+ ...
3
9
27
B. Write the repeating decimal as the ratio of two integers.
0.18
Problem 6
Find the equation of conic with the graph shown below:
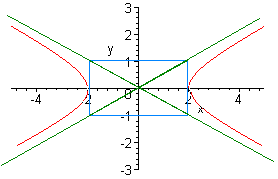
Problem 7
Use Pascal's Triangle to expand
(3 - 2x)4
Problem 8
Solve the following:
A. log6(x - 5) + log6(x) = 2
B. 22x-1 = 53x-2
C. Use a calculator to evaluate log7 51
Problem 9
The clarity C (in feet) of Lake Tahoe t years since 1990 can be modeled by the equation
C(t) = 45e-t/25
A. How clear was the lake in 1995.
B. When will the clarity of the lake only be 5 feet?
Problem 10
Solve the following system of nonlinear equations:
x2 + y2 = 25
3x + 5y = 15
Problem 11
Graph the solution to the system of nonlinear inequalities
x2 - y2 < 1
x
> y2