Name                                    

MAT 154A Practice Exam 3

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Do all your work and give all your answers on you own sheet of paper.  Show your work.

Problem 1

Sketch the graphs of the given functions:

A.                             x2
                               + 4y2 = 1
                        9            

Solution

First notice that this is an ellipse since both coefficients are positive.  Putting the 4 in the denominator gives

        x2          y2
               +               =  1
        9          1/4      

So that

        a  =  3        b  =  1/2

The vertices of the ellipse are at 

        (3,0), (-3,0), (0,1/2) (0,-1/2)

Now plot the points and sketch the ellipse.

       

B.     x2 + y2 + 2x - 4y - 4  =  0    

Solution

First complete the two squares

        x2 + 2x + (1 - 1) +  y2 - 4y + (4 - 4) - 4  =  0   Reordering and adding and subtracting b/2 to both

        (x + 1)2 + (y - 2)2  =  9        Factoring, adding -1 - 4 - 4 = -9, and adding 9 to both sides

We recognize this as a circle with center (-1,2) and radius 3.  The graph is given below

 

Problem 2

A. Find the first four terms of the sequence whose general term is given. Then find the 100th term. 

        an  =  n - 1/n

Solution

We have

        a1  =  1 - 1/1  =  0

        a2  =  2 - 1/2  =  3/2

        a3  =  3 - 1/3  =  8/3

        a4  =  4 - 1/4  =  15/4

        a100  =  100 - 1/100  =  9999/100

B. Expand and simplify

       

Solution

We plug in 2, 3, 4, and 5 to get

        [2(2) + 1] + [2(3) + 1] + [2(4) + 1] + [2(5) + 1] 

        =  5 + 7 + 9 + 11  =  32

       

C.   Write the series in summation notation

        1       2       3       4
            +       +       +       + ...
        2       3        4       5                       

Solution

The numerator is just n and the denominator is n + 1.  Where n starts at 1 and continues to infinity.  In summation notation, this becomes

       

       

 

 

Problem 3 

A)     Find the indicated unknown

        8, 13, 18, 23, ..., 88            n  =  ?

Solution

This is an arithmetic sequence since 

        13 - 8  = 18 - 3  =  23 - 18  =  5

The common difference is d  =  5.

The first term is 8, so the general formula is

        an  =  8 + 5(n - 1)

The last term is 88, so we set

        88  =  8 + 5(n - 1)    

        80  =  5(n - 1)    Subtract 8

        16  =  n - 1        divide by 5

        n  =  17        add 1

       

B)    Find the sum of the given series

       

Solution

This is an arithmetic sequence with 

        d  =  3       a1  =  3        and         n  =  54

We use the sum of an arithmetic sequence formula to find the 54th term.

        a54  =  3 + 3(54 - 1)  =  162

The sum is 

        n/2 (a1 + an)

        54/2 (3 + 162)  =  4455

Problem 4 

A.  Find the indicated unknown

        a1  =  5,   a5  =  0.008        r  =  ?

Solution

This is a geometric sequence with 

        an  =  a1rn-1

We have

        0.008  =  5r5-1

        0.0016  =  r4        Dividing by 5

         r  =  (0.0016)1/4  =  0.2

B.  A rubber ball is dropped on a hard surface and bounces to a height of 200 ft.  On each rebound it bounces 95% as high as on the previous bounce.  How high does the ball bounce on the 20th bounce?

Solution

We first write the first few terms of the sequence, which represents the height of the nth bounce.

        a1  =  200        a2  =  .95(200)      a3  =  .95(.95(200))  =  .952(200)

We see that this is a geometric sequence with 

        an  =  200(.95)n-1 

We want the height of the 20th bounce.  We have

        a20  =  200(.95)19  =  75.5

The ball bounces about 75.5 feet on the 20th bounce

Problem 5 

A.  Find the sum of the infinite series if it exists.

              1       1         1       
       1+       +        +         + ...
              3       9         27                       

Solution

This is a geometric sequence with first term 1 and common ratio r  =  1/3. We have

                          a1                   1                        1              3
             S  =                   =                    =                    =         
                         1 - r               1 - 1/3                2/3            2

B.  Write the repeating decimal as the ratio of two integers.

        0.18   

 

Solution

We write

        0.18   =  .18 + .0018 + .000018 + .00000018 +...

This is an infinite geometric sequence with 

        a1  =  .18  =  18/100    and     r  =  .01  =  1/100

We have 

                    18/100            
        S  =                                
                   1 - 1/100

                    18            
         =                           Multiply top and bottom by 100     
                  100 - 1

                 18               2
          =              =            
                 99              11

Problem 6 

Find the equation of conic with the graph shown below:

 

 

Solution

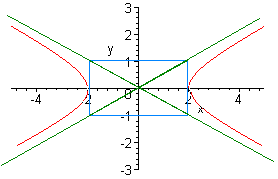
Since this is a hyperbola centered at the origin, we need to determine a, b, and the signs.  Since the hyperbola has x intercepts, the coefficient in front of x is positive.  We have

        a  =  2,        b  =  1

The equation is 

     

        x2         y2
               -             =  1
        4          1      

   or

        x2 - 4y2  =  4

 

 

Problem 7 

Use Pascal's Triangle to expand

(3 - 2x)4

Solution

First create Pascal's Triangle

                   1
               1     1
           1      2     1
       1      3      3     1
    1    4       6      4      1

Next write out the powers starting out with the fourth power for the first term and the 0th power for the second.  The first term powers decrease by one for each successive term and the second term powers increase by one for each successive term so that the sum of the two powers stays fixed at four.

34         33 (-2x)        32 (-2x)2        3(-2x)3       (-2x)4

Next insert the numbers from the fifth line of Pascal's triangle.  Also add "+" signs because we are adding the terms.

(1)34   +   (4) 33 (-2x)   +    (6) 32 (-2x)2   +    (4) 3(-2x)3  +    (1) (-2x)4

Next, perform the exponentiation.

81 + (4)(27)(-2)x + (6)(9)(4)x2 + (4)(3)(-8)x3 + (16)x4

Finally multiply out the coefficients

81 - 216x + 216x2 - 96x3 + 16x4

or

16x4 - 96x3 + 216x2 - 216x + 81

 

Problem 8 

Solve the following:

A.     log6(x - 5) + log6(x)  =  2      

Solution

Use the sum to product rule of logarithms

        log6[(x)(x - 5)]  =  2    

        (x)(x - 5)  =  62    Remember logs are exponents

        x2 - 5x  =  36        Multiplying out

        x2 - 5x - 36  =  0      Subtracting 36 from both sides

        (x - 9)(x + 4)  =  0

        x  =  9    or     x  =  4

Notice that 4 is not a solution since it is not in the domain of log6(x - 5).  9 is a solution, as you can verify with your calculator.

B.  22x-1  =  53x-2  

Solution

Take ln of both sides

        ln 22x-1  =  ln 53x-2  

        (2x + 1) ln 2  =  (3x - 2) ln 5    Using the power to product rule of logs

        2x ln 2  +  ln2    =    3x ln 5  -  2 ln 5    Multiplying out

        2x ln 2  -  3x ln 5    =    -ln 2  -  2 ln 5    Separating x terms to the left and others to the right

        x(2 ln 2  -  3 ln 5)    =    -ln 2  -  2 ln 5    Factoring out the x

                  -ln 2  -  2 ln 5
        x  =                                  =  1.1365    Dividing by 2 ln 2  -  3 ln 5  
                   2 ln 2  -  3 ln 5

C.  Use a calculator to evaluate  log7 51

Solution

First use the change of base formula

                            log 51  
        log7 51  =                      
                            log 7  

Now put this in your calculator to get

        2.02055867514

 

Problem 9 

The clarity C (in feet) of Lake Tahoe t  years since 1990 can be modeled by the equation

        C(t)  =  45e-t/25

A.      How clear was the lake in 1995.

Solution

The year 1995 corresponds to t  =  5.  Plug this in for t to get

        C(5)  =  45e-5/25  =  36.84

The clarity of the lake was 36.84 feet in 1995

        

B.     When will the clarity of the lake only be 5 feet?

Solution

Now plug in 5 for C to get

        5  =  45e-t/25

        1/9  =  e-t/25        Dividing both sides by 45

        ln(1/9)  =  ln(e-t/25)      Taking the ln of both sides

        ln(1/9)  =  -t/25        Cancelling the ln and the e

        -25 ln(1/9)  =  t        Multiplying both sides by -25

        t  =  54.93

Now turn this back into a date by adding it to 1990

        1990 + 54.93  =  2044.93

We can say that towards the end of the year 2044 the clarity of the lake will be only 5 feet.

 

 

Problem 10

Solve the following system of nonlinear equations:

        x2 + y2  =  25

        3x + 5y  =  15

  Solution

We first solve the second equation for x by dividing by subtracting 5y and dividing by 3

        3x  =  15 - 5y

        x  =  5 - 5/3 y

Now substitute into the first equation to get

        (5 - 5/3 y)2 + y2  =  25

        25  -  50/3 y + 25/9 y2 + y2  =  25        FOIL

        -50/3 y + 25/9 y2 + y2  =  0        Subtracting 25 from both sides

        -150y + 25y2 + 9y2  =  0        Multiplying both sided by 9

         34y2 - 150y  =  0        Combining like terms

          2y(17y - 75)  =  0    Factoring out the GCF

           y  =  0        or      y  =  75/17  =  4.41

Now plug these solutions back into the equation

           x  =  5 - 5/3 y

to get

           x  =  5 - 5/3 (0)        or        x  =  5 - 5/3 (75/17)

           x  =  5        or        x  =  5 - 125/17  =  -40/17  =  2.35

Our two solutions are (5,0) and (2.35,4.41)

 

Problem 11

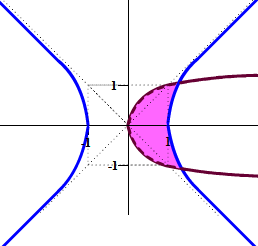
Graph the solution to the system of nonlinear inequalities

x2 - y2  <  1

x  >  y2

Solution

First we graph the two curves.  Graph the first with a solid curve and the second with a dashed curve, since when the inequality includes "=" the curve is included and we write a solid curve.  When it doe not include the "=", we write a dashed curve.  The first curve is a hyperbola with x-intercepts since the positive belongs to the x term.  The second curve is a sideways parabola.  The graph is shown below.

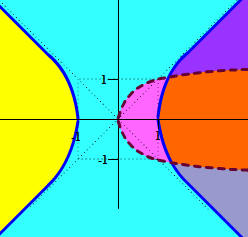
Graph of the hyperbola and parabola with the six regions 

We can see that there are six regions.  Next choose test points to see which regions should be shaded.  The left region's test point is (-2,0).  The first inequality is false thus we do not shade this region.  The middle region's test point is (0,2).  The second inequality is false, so this region also should not be shaded.  The next region's test point is (0.5,0).  Both inequalities are true, so we shade this region.  The top right region's test point is (2,2).  The second inequality is false, so we do not shade this region.  The top bottom region's test point is (2,-2).  the second inequality is false, so we do not shade this region.  The right region's test point is (2,0).  The first inequality is false, so this region is not included.  Thus the only region that is included is the region to the right of the parabola and the left of the right branch of the hyperbola.  The solution graph is shown below.

Solution to the inequality with the right of the parabola and left of the right branch of the hyperbola shaded in