Name                                    

MATH 154 PRACTICE FINAL

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Do all of your work and show your solutions on your own sheet of paper.  Show your work.

  Printable Key

Problem 1  

Solve

  Solution

Problem 2 

A square floppy disk is of length 4.8 in across the diagonal.  Determine the length of the side of the disk.

  Solution

Problem 3  

Determine (f ^o g)(x)    if    f(x)  =  2x - 1     and    g(x)  x²+ 2x

  Solution

Problem 4  

Graph the quadratic function.  Label the intercepts and the vertex.  Then put the parabola in standard form and explain in complete sentences how the parabola y = x²  has “shifted”.

        y  =  x² - 2x - 3

  Solution

Problem 5 

Sketch the graph of the following

A.           4x + 9y  =  36

Solution

B. 

                 y²          x² 
                        -              =  1               
                25           4

Solution

C.      y  =  |x - 4|

Solution

D.      y  =  3^x + 2

Solution

E.       y  =  log₂(-x)

Solution

F.        x² + y² - 4y  =  12

Solution

Problem 6

Determine whether the given function is 1-1.  If it is find its inverse

A.     f(x)  =  (x - 2)²

Solution

B.     f(x)  =  4 - 3x

  Solution

Problem 7  Solve

A.     2^x  =  3^x-1   

Solution

B.      log(37x - 1)  =  log(2x + 5) + 1

  Solution

Problem 8    Expand the following logarithm.  Simplify where possible.  Assume all variables are such that all expressions are defined. 

  Solution

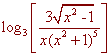
Problem 9  Solve the system.  then describe in words what is happening geometrically.

        x² + y²  =  25

        2x + y  =  5

  Solution

Problem 10 

Write the following series in summation notation.

          3         4           5           6                 12
                +         +           +          + ... +                
          4         9          16         25               121

  Solution

Problem 11  

Find the indicated unknown for the arithmetic sequence.

        S₁₅  =  -300,    a₁₅  =  -8,    a₂₃  =  ?

  Solution

Problem 12 

Fifteen years ago 10,000 tons of trash were put into the landfall.  Each year, because of growth, the trash used by the community is increased 10% over the previous year.  How much total trash is in the landfill today?  (use a geometric series)

  Solution

Problem 13 

Answer the following true or false and explain your answer.

A.      The only conic that is the graph of a function is the parabola  y  =  ax² + bx + c  

Solution

B.         

Solution

C.       log₄(1 - x)  is undefined at x = -3.  

Solution