Name                                    

MATH 154 PRACTICE FINAL

Please work out each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Do all of your work and show your solutions on your own sheet of paper.  Show your work.

 

Problem 1  

Solve

  Solution 

We first subtract 2 from both sides

          

Now square both sides to get

        x + 4  =  (x - 2)2  =  x2 - 4x + 4

        x2 - 5x =  0        Subtracting x + 4 from both sides

        x(x - 5)  =  0        Factoring

        x  =  0        or        x  = 1        By the zero product theorem

Notice that when you plug in 0 you get  2  =  -2 which is false.  However x  =  5 checks out.  Hence the solution is 

        x  =  5

Problem 2 

A square  is of length 4.8 in across the diagonal.  Determine the length of the side of the square.

  Solution

We first sketch the picture

Now use the Pythagorean theorem to get

        x2 + x2  =  4.82

        2x2  =  23.04        Combining like terms

        x2  =  11.52        Dividing by 2

        x  =  3.4         Taking the square root

The length of the side of the square is approximately 3.4 inches

Problem 3  

Determine (f o g)(x)    if    f(x)  =  2x - 1     and    g(x)  x2+ 2x

  Solution

We have 

        f o g(x)  =  f(g(x))  

        =  f(x2 + 2x)  =  2(x2 + 2x) - 1  

        =  2x2 + 4x - 1

Problem 4  

Graph the quadratic function.  Label the intercepts and the vertex.  Then put the parabola in standard form and explain in complete sentences how the parabola y = x2  has “shifted”.

        y  =  x2 - 2x - 3

  Solution 

First find the y-intercept by plugging in 0 for x

        (0,-3)

Next find the x-intercepts by plugging in 0 for y

        0  =  x2 - 2x - 3  =  (x - 3)(x + 1)

        x  =  3        or         x  =  -1

The x-intercepts are 

        (3,0)        and        (-1,0)

Now put it into standard form by completing the square

        y  =  x2 - 2x - 3  =  x2 - 2x + 1 - 1 - 3    adding and subtracting (-2/2)2  =  1

        =  (x - 1)2 - 4

Hence the vertex is at 

        (1,-4)

The standard parabola is shifted 1 to the right and 4 down.  The graph is shown below

       

Problem 5 

Sketch the graph of the following

A.           4x + 9y  =  36

Solution

We see that this is a line since it has no square terms.  We find the x-intercept by plugging in 0 for y to get

        4(0) + 9y  =  36

        (9,0)

and the y-intercept by plugging in 0 for x to get 

        4x + 9(0)  =  36

        (0,4)

Now plot the points and connect the dots.

       

B. 

                 y2          x2 
                        -              =  1               
                25           4

Solution

This is a hyperbola since both x and y are squared and the signs are different.  We have 

        a  =  2        and         b  =  5        Square roots of 4 and 25

The vertices are on the y-axis since the positive belongs to the y-term.  Now draw the fundamental rectangle, the diagonals, and then sketch the hyperbola.

       

C.      y  =  |x - 4|

Solution

This is an absolute value graph (shaped like a "V").  The vertex is shifted to the right by 4 so is at the point (4,0).  The graph is pictured below

       

D.      y  =  3x + 2

Solution

This is an exponential with base greater than one.  It is shifted 2 up.  Plugging in 0 gives 

        30 + 2  =  1 + 2  =  3

Plugging in 1 gives 

        31 + 2  =  3 + 5  =  5

Now plot the points and connect with an exponential graph.

       

E.       y  =  log2(-x)

Solution

This is the graph of a logarithm function with base greater then 2.  The "-" sign reflects the graph about the y-axis.  Hence we can only put in negative values for x.  When x  =  -1, we get 

        y  =  log2(-(-1))  =  log21  =  0

When x =  -2, we get

        y  =  log2(-(-2))  =  log22  =  1

We now plot the points and connect with a logarithm curve.

       

F.        x2 + y2 - 4y  =  12

Solution

This is a circle, since the coefficients are both the same number (1).  We complete the square to get

        x2 + y2 - 4y + 4 =  12 + 4    Adding (-2)2  =  4 to both sides

        x2 + (y - 2)2 =  16

Hence the center of the circle is at 

        C  =  (0,2)

and the radius is 

        r  =  4        The square root of 16

Now draw the circle

       

 

Problem 6

Determine whether the given function is 1-1.  If it is find its inverse

A.     f(x)  =  (x - 2)2

Solution

This is a parabola, so it does not pass the horizontal line test.  In particular

        f(1)  =  f(3)  = 1

so it is not 1-1 hence there is not inverse function.

B.     f(x)  =  4 - 3x

Solution

  This is a non-vertical line, so it does pass the horizontal line test.  Now switch the variables and solve for y.

        x  =  4 - 3y

        x - 4  =  3y            Subtracting 4 from both sides

        x/3 - 4/3  =  y        Divide each term by 3

        f -1(x)  =  x/3 - 4/3

Problem 7  Solve

A.     2x  =  3x-1   

Solution

We take log of both sides

        log(2x)  =  log(3x-1)

        x log 2  =  (x - 1) log 3        Using the power rule

        x log 2  =  x log 3  - log 3    Multiplying through

        x log 2 - x log 3  =  -log3    Subtracting x log 3 from both sides

        x(log 2 - log 3)  =  -log 3    Factoring out an x

                      -log 3
  x  =                           =  2.7        Dividing by log 2 - log 3 and 
             log 2 - log 3                       using a calculator

B.      log(37x - 1)  =  log(2x + 5) + 1

  Solution

Subtract the logs to get

        log(37x - 1)  -  log(2x + 5)  =  1  

                  37x - 1
         log                     =  1        Using the difference to quotient rule
                   2x + 5                 

            37x - 1
                             =  101  =  10       Logs are exponents
             2x + 5               

        37x - 1  =  10(2x + 5)  =  20x + 50    Multiplying by the denominator

        17x  =  51        Subtracting 20x and adding 1 to both sides

          x  =  3        Dividing by 17

        

Problem 8    Expand the following logarithm.  Simplify where possible.  Assume all variables are such that all expressions are defined. 

         

  Solution

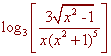
We use the quotient and product rules to get

       

Now cancel the log3 with the 3, and write the square root as an exponent to get

        1 + log(x2 - 1)1/2 - log x - log(x2 + 1)5

Now use the power rule of logs

        1 + 1/2 log(x2 - 1) - log x - 5log(x2 + 1)

Now factor to get

         1 + 1/2 log[(x + 1)(x - 1)] - log x - 5log(x2 + 1)  

Finally use the product to sum formula to get

         1 + 1/2 log(x + 1) + 1/2 log(x - 1) - log x - 5log(x2 + 1)  

 

 

Problem 9  Solve the system.  then describe in words what is happening geometrically.

        x2 + y2  =  25

        2x + y  =  5

  Solution

Solving the second equation for y we get

        y  =  5 - 2x

Substituting into the first equation gives

        x2 + (5 - 2x)2  =  25

        x2 + 25 - 20x + 4x2  =  25    FOIL

        5x2 - 20x + 25  =  25        Combining like terms

        5x2 - 20x  =  0        Subtracting 25 from both sides

        5x(x - 4)  =  0        Factoring

        x  =  0         or         x  =  4        Zero product property

Plugging in to the y  =  5 - 2x gives

        y  =  5 - 2(0)         or        y  =  5 - 2(4)

        y  =  5        or        y  =  -3

Gives the points

        (0,5)        and         (4,-3)

A quick check and we see that these two point satisfy both equations.

 

Problem 10 

Write the following series in summation notation.

          3         4           5           6                 12
                +         +           +          + ... +                
          4         9          16         25               121

  Solution

First we see that the numerator is arithmetic with 

        a1  =  3    and     d  =  1

We see that the denominator is the square of  n + 1.  Hence

                    3 + 1(n - 1)
        an  =                                
                       (n + 1)2 

The series begins at n  =  1 and ends at n  =  10 (since (10 + 1)2  =  121) We write

       

 

Problem 11  

Find the indicated unknown for the arithmetic sequence.

        S15  =  300,    a15  =  -8,    a23  =  ?

  Solution

        We use the formula

                      n(a1 + a15)  
        S15  =                          
                              2

Plugging in, we get

                      15(a1 - 8)  
        300  =                          
                              2

        600  =  15(a1 - 8)  =  15a1 - 120    Multiplying both sides by 2

        720  =  15a1          Adding 450 to both sides

        a1  =  48

Now we find d using a15 

        a15  =  a1 + d(15 - 1)

        -8  =  48 + 14d

        14d  =  -56        Subtracting 48 from both sides

        d  =  -4

Now use d and a1 to find a23

        a23  =  48 - 4(23 - 1)  =  -40

Problem 12 

Fifteen years ago 10,000 tons of trash were put into the landfall.  Each year, because of growth, the trash used by the community is increased 10% over the previous year.  How much total trash is in the landfill today?  (use a geometric series)

  Solution

We find the first few terms of the series

        a1  =  10,000

        a2  =  10,000 + (.1)(10,000)  =  (1.1)(10,000)

        a3  =  (1.1)(1.1)(10,000)  =  (1.12)(10,000)

We get the geometric series with 

        r  =  1.1        a1  =  10,000         and        n  =  15

Now use the geometric series formula to get

                       a1(1 - rn)
        Sn  =                              
                           1 - r

                       10,000(1 - 1.115)
        Sn  =                                         =  317,725
                           1 - 1.1

There is 317,175 tons of trash in the landfill today

 

Problem 13 

Answer the following true or false and explain your answer.

A.      The only conic that is the graph of a function is the parabola  y  =  ax2 + bx + c  

Solution

True, ellipses, hyperbolas, and circles are not graphs of functions since they do not pass the vertical line test.

B.         

Solution

False,  the series diverges (equals infinity) since 2 > 1.

C.       log4(1 - x)  is undefined at x = -3.  

Solution

False

        log4(1 - (-3))  =  log4(4)  =  1