Exercises for Absolute Value Inequalities
1. The absolute value inequality |ax + b| < c has exactly one solution if c is zero.
3. The absolute value inequality |ax + b| < c has exactly an infinite number of solutions if c is positive.
For problems 4 through 7 answer true or false and explain your reasoning.
5. The solution to |x + b| < 1 includes only a single interval without its endpoints.
True, notice that for very large values of x, the statement is false, hence the solution is between the endpoints. Since the inequality is "<" the solution does not include the endpoints.
7. Every value of x satisfies the inequality |2x + b| > 0.
False, if x = -b/2, the endpoints are not included.
For problems 8 through 27, solve the inequality. Show the solution set in both interval notation and on a number line.
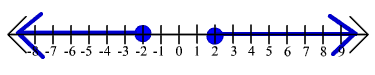
9. |x| > 2
(-
,-2] U [2,)
11. |x| < 0
x = 0
13. |x + 2| < 3
(-5,1)
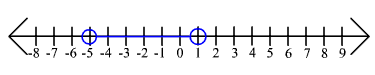
15. |x + 5| > 2
(-
,-7] U [-3,)
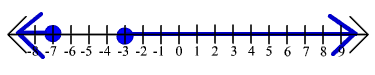
17. |3x - 9| > 15
(-
,-2) U (8,)
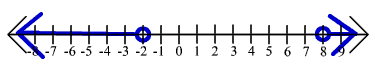
19. |3x - 2| > 5
(-
,-1] U [7/3,)
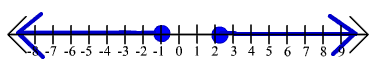
21. 2|5x + 1| - 3 < 5
(-1,3/5)
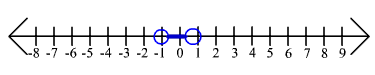
23. 7|2x + 1| + 3 < 1
No Solution
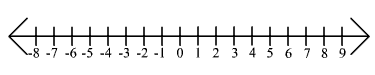
25. |2.5x - 0.5| + 1.5 > 3.5
(-
,-0.6) U (1,)
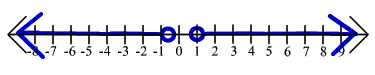
27. 1
3
|3x - 5| <
2
4
[7/6,13/6]
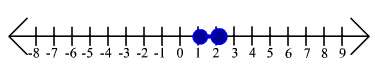
For exercises 28 through 31 write down an absolute value inequality that had the solution shown.
29.
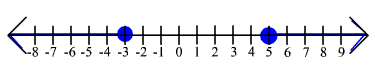
|x - 1| > 4
31. x < 2 or x > 8
|x - 5| > 3