Exercises for Absolute Value Inequalities
Solutions to the odd exercises
1. The absolute value inequality |ax + b| < c has exactly one solution if c is _________________.
2. The absolute value inequality |ax + b| < c has no solution if c is _________________.
3. The absolute value inequality |ax + b| < c has exactly an infinite number of solutions if c is _________________.
For problems 4 through 7 answer true or false and explain your reasoning.
4. The solution to |x + b| > 1 includes 2 disconnected pieces, one from negative infinitive to a value and the other from a different value to infinity.
5. The solution to |x + b| < 1 includes only a single interval without its endpoints.
6. The inequality |3x - b| < 0 has exactly one solution.
7. Every value of x satisfies the inequality |2x + b| > 0.
For problems 8 through 27, solve the inequality. Show the solution set in both interval notation and on a number line.
8. |x| < 3
9. |x| > 2
10. |x| > -4
11. |x| < 0
12. |x - 1| < 4
13. |x + 2| < 3
14. |x + 4| > 6
15. |x + 5| > 2
16. |2x - 4| < 12
17. |3x - 9| > 15
18. |4x + 3| < 6
19. |3x - 2| > 5
20. 3|2x - 3| + 1 > 2
21. 2|5x + 1| - 3 < 5
22. 5|4x - 6| + 8 > 2
23. 7|2x + 1| + 3 < 1
24. |0.1x + 1.2| < 1.1
25. |2.5x - 0.5| + 1.5 > 3.5
26. 3
2
|2x + 1| <
4
3
27. 1
3
|3x - 5| <
2
4
For exercises 28 through 31 write down an absolute value inequality that had the solution shown.
28. 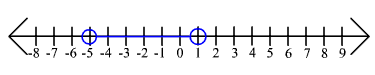
29.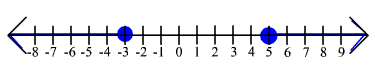
30. (-4,6)
31. x < 2 or x > 8
Back to information on Absolute Values