Solutions to the Odd Exercises for Functions
1. A function is a rule that assigns to each element of a domain set to a unique element of a range set.
For exercises 3 through 6 answer either "True" or "False" and explain how you arrived at your conclusion.
3. The graph of a function can never have more than one y-intercept.
True, since if it had more than 1 y-intercept, then the x-value 0 would be assigned to more than one y-value.
5. Every line is the graph of a function.
False, vertical lines are not graphs of functions.
For exercises 7 - 10, a relation is given in the form of ordered pairs. Determine the domain, the range, state whether the relation is a function.
7. (1,2), (2,3), (3,4), (4,5), (7,7)
Domain = {1,2,3,4,7} Range = {2,3,4,5,7}
This relation is a function.
9. (0,2), (1,6), (1,5), (9,12), (10,11)
Domain = {0,1,9,10} Range = {2,5,6,11,12}
This relation is not a function since the value 1 gets assigned to two numbers.
For exercises 11 through 14, graphs are given. Determine whether the graph is a function and explain your reasoning.
11. 
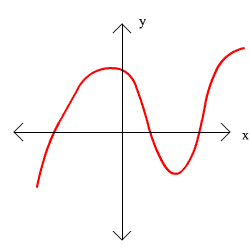This is a function
13.
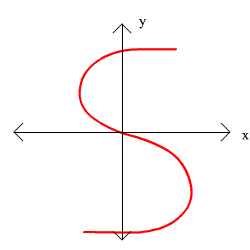This is not a function
For exercises 15 - 18, determine the domain and range and state whether the relation described is a function.
15. Every person is assigned to his or her biological mother.
Domain: All people, Range: All mothers. This is a function.
17. Every word is assigned that are generated during a Google search.
Domain: All words, Range: All URL's. This is not a function.
For exercises 19 - 28, let f(x) = 3x - 4 and g(x) = x2 + x and h(x) = 3. Find the indicated value.
19. f(2)
2
21. h(-4)
12
23. g(x + 1)
x2 + 3x + 1
25. (f - g)(4)
-12
27. (f / g )(2)
1/3
29. g(x + 1) - g(x)
2x + 2
31. (g h)(5)
90
For exercises 32 through 39, use the graphs shown below to approximate the indicated value.
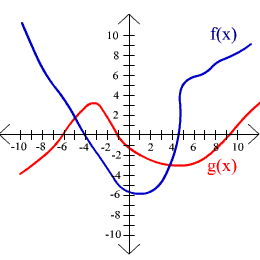
33. g(-3)
3
35. g(8)
1
37. (f - g)(-5)
0
39. (f / g)(6)
-2
Find the domain of the functions given in exercises 40 - 43.
41. f(x) = x2 + x - 2
All real numbers
43.
3x
- 4
f(x) =
5x - 1
All real numbers except for x = 1/5
For exercises 44 - 47 use the given graphs to find the domain and the range.
45.
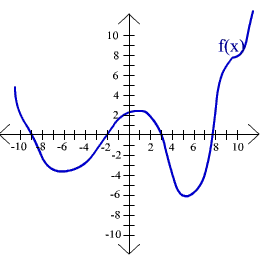Range is real numbers
greater than -6.
47.
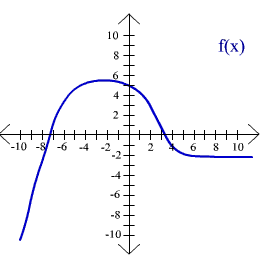Range is all real
numbers less than 6.