Exercises for Functions
Solutions to the Odd Exercises
1. A function is ______________________________________________________________________+__________.
2. The vertical line test says that a graph is a graph of a function if every vertical line passes through the graph ___________.
For exercises 3 through 6 answer either "True" or "False" and explain how you arrived at your conclusion.
3. The graph of a function can never have more than one y-intercept.
4. The graph of a function can never have more than one x-intercept.
5. Every line is the graph of a function.
6. Circles are never graphs of functions.
For exercises 7 - 10, a relation is given in the form of ordered pairs. Determine the domain, the range, state whether the relation is a function.
7. (1,2), (2,3), (3,4), (4,5), (7,7)
8. (-1,4), (0,5), (1,4), (2,3)
9. (0,2), (1,6), (1,5), (9,12), (10,11)
10. (-3,-1), (-1,-3), (0,5), (2,1)
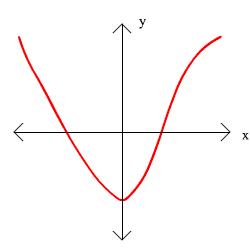
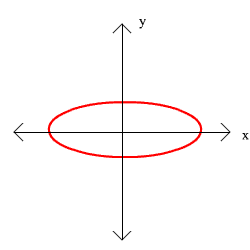
For exercises 11 through 14, graphs are given. Determine whether the graph is a function and explain your reasoning.
11. 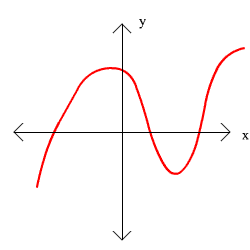 12.
12.
13.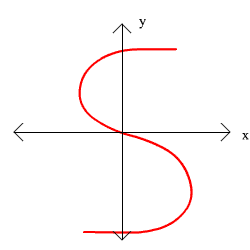 14.
14. 
For exercises 15 - 18, determine the domain and range and state whether the relation described is a function.
15. Every person is assigned to his or her biological mother.
16. Every mother is assigned to her children.
17. Every word is assigned that are generated during a Google search.
18. Every Hotmail account user name is assigned to the corresponding password.
For exercises 19 - 28, let f(x) = 3x - 4 and g(x) = x2 + x and h(x) = 3. Find the indicated value.
19. f(2)
20. g(-1)
21. h(-4)
22. f(a - 1)
23. g(x + 1)
24. (f + g)(3)
25. (f - g)(4)
26. (f g)(1)
27. (f / g )(2)
28. 3f(x) - 2g(x)
29. g(x + 1) - g(x)
30. (f + h)(2)
31. (g h)(5)
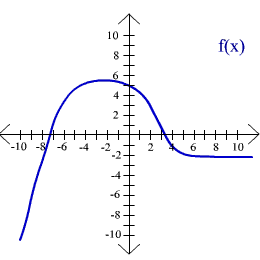
For exercises 32 through 39, use the graphs shown below to approximate the indicated value.
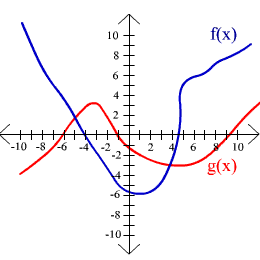
32. f(-10)
33. g(-3)
34. f(-1)
36. g(8)
36. (f + g)(0)
37. (f - g)(-5)
38. (f g)(2)
39. (f / g)(6)
Find the domain of the functions given in exercises 40 - 43.
40. f(x) = 3x - 4
41. f(x) = x2 + x - 2
42.
x - 2
f(x) =
x + 2
43.
3x
- 4
f(x) =
5x - 1
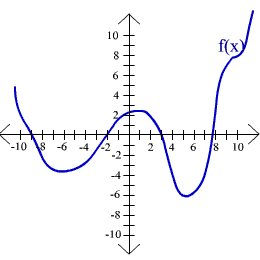
For exercises 44 - 47 use the given graphs to find the range of f(x).
44. 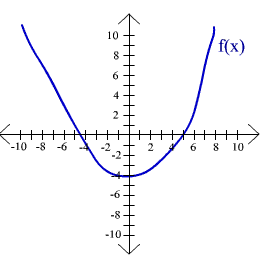 45.
45. 
46. 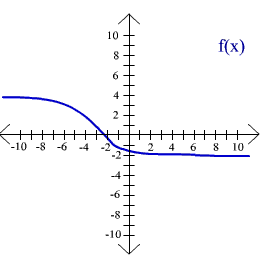 47.
47. 
e-mail Questions and Suggestions