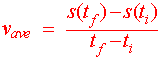A Preview of Calculus

Local graph experiment  

Try this experiment: Write down an arbitrary function and an arbitrary value of x.  Enter the function into a graphing calculator and zoom in on the point.  You will notice that your calculator shows a line.  Now,  use two points on the graph to compute the slope of the curve produced.  A large part of calculus involves investigating this slope and its implications.


Click here for an interactive applet that helps you work this experiment

Speed  

Example

Suppose that you are cycling on Highway 50 and clock the following times:

Time (t)	Distance (s)
1:00	0
1:15	6
1:30	9
2:00	16

Then your average velocity is defined by

where t_f is the time at the end of the ride and t_i is the time at the beginning of the ride and s(t) is the position at time t.  The above expression is called the difference quotient.

1. Using 1:00 as time 0 minutes, we can compute the average velocity
   
                     16 - 0
      v_ave  =                     =   0.267   miles per minute
                      60 - 0 
   
   

2. How fast is the bicycle moving when t = 15 minutes?  We can compute the average velocity from 0 to 15 minutes by
   
                        6 - 0
      v_ave  =                     =   0.4   miles per minute
                      15 - 0 
      
   
   or we can compute the average velocity from 15 to 30 by
   
                         9 - 6
      v_ave  =                     =   0.2   miles per minute
                      30 - 15 
   
   
   Both of these are estimates.  We can get a better estimate by measuring points closer to time 15, but we can still never get the exact velocity.  If we have a formula we can use the ideas learned from the calculator exercise and note that the slope of the tangent line is the instantaneous velocity. 

Integral Calculus

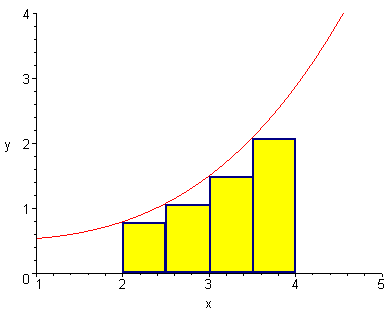
How does one find the area under a curve?  The easiest area formula we know is the area of a rectangle (base)(height).  If we approximate the area under a curve by drawing several small rectangles (See the diagram), then we will have a close approximation.  We can never get the exact area this way, but we can come as close to the area as we wish.  At the end of this quarter we will learn to find the exact area if we are given a formula.


               

Back to Math 105 Home Page

e-mail Questions and Suggestions