Practice Exam I

Key

Problem 1

Consider the graphs shown below.  Find

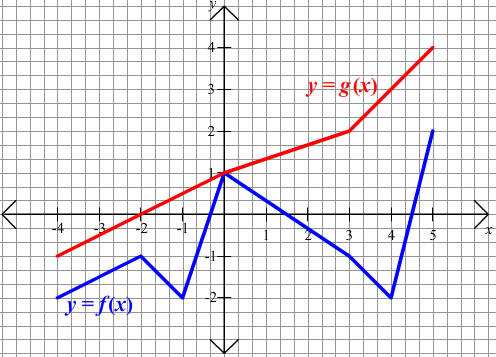
Graphs of f(x) and g(x) 

A.  Find f o g(4)

B.  Find g^-1(2)

C.  Sketch the graph of y = g -1(x)

 

Problem 2

Let

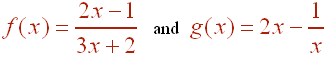
f(x) = (2x-1)/(3x+2) and g(x) = 2x - 1/x

A.  Find gof(1)

B.  Find and simplify fog(x)

C.  Find f -1(x)

 

Problem 3

Graph the following.  Then find the domain, range, and asymptote.

A.  f(x) = 1-2^(x-3)

B.  f(x)=ln(2-x)

C.  2log_(1/3)(x+1)

 

Problem 4

Solve the following equations

A. 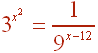 3^(x^2) = 1/9^(x-12)

B.  log_x(9)=2

C.  2log_2(x-1)=3-log_2(x)

D.  5^(x-1) = 3^(2x)

 

Problem 5

A.  Change the exponential statement to an equivalent statement involving a logarithm.

5^x = 6

B.  Change the logarithmic statement to an equivalent statement involving an exponent.

ln7 = x

 

Problem 6

Let ln(3) = a  and ln(6) = b.  Write the following in terms of a and b.

A.  ln(2)

B.  ln(54)

C.  ln(root(18))

 

Problem 7

Write the expression as a sum or difference of logarithms. Express powers as factors and simplify all numbers.

log[ 100x^3 (x-1)^5 / cubeRoot(x+2) ]

 

Problem 8

This year, it costs the average family $1000 per month for health insurance.  If the inflation rate is 9% per year (compounded continuously), how long will it take until the cost of health insurance is $1500 per month?

 

 

Problem 9

A loan company offers a $5,000 loan where the customer makes no monthly payments, but must pay back $7,000 in four years.  Assuming a monthly compounding period, what is the annual interest on this loan?

 

Problem 10

A culture of bacteria obeys the law of uninhibited growth.  At noon, there were 200 bacteria present and at 1:00 PM there were 250 present.

A.  How many bacteria will be present at 3:00 PM?

B.  What is the doubling time for this bacteria?

 

Problem 11

The half-life of radioactive Cobalt-60 is 5.27 years.  If a terrorist detonates a Cobalt-60 bomb, ground zero will remain uninhabitable until only 2% of the Cobalt-60 remains.  How long will it be until ground zero becomes inhabitable?

 

Problem 12

A victim whose body temperature before she was murdered was 98.6 degrees Fahrenheit.  The temperature of the room that she was murdered in has been a constant temperature of 65 degrees Fahrenheit since the time of death.  At 3:00 PM the body was found to have a temperature of 80 degrees Fahrenheit.  At 4:00 PM the body had a temperature of 70 degrees Fahrenheit.  What was the time of death?

 

Problem 13

  The world population P(t) (in billions) t years since 1900 is given by

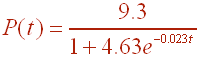
P(t) = 9.3/(1+4.63 e^(-0.023t))

A.  What is the carrying capacity and the rate of growth?

B.  What was the population in 1900?

C.  What was the population in 2010?

D.  When will the population reach 9 billion?