Practice Exam I

Problem 1

Consider the graphs shown below.  Find

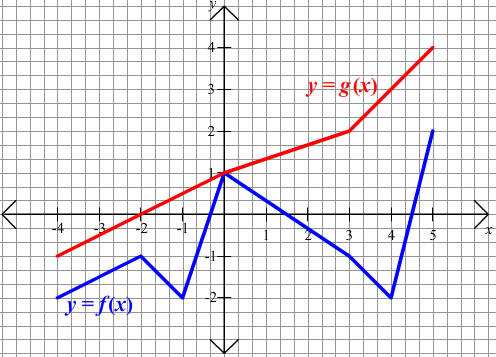
A.  Find

Solution

First find g(4).  Notice that the graph of y = g(x) passes through the point (4,3).  Thus g(4) = 3.  Now plug 3 into f and find f(3).  Notice that the graph of y = f(x) passes through the point (3,-1).  thus f(3) = -1.  Therefore

f(g(4)) = f(3) = -1

B.  Find

Solution

To find the inverse evaluated at 2, we are looking for the value of x such at y = 2.  Notice that the point (3,2) is on the graph of g.  Therefore g ^-1(2) = 3

C.  Sketch the graph of y = g ^-1(x)

To graph the inverse function, we reflect across the line y = x.  Also if the point (x,y) is on the graph of g, then the point (y,x) will be on the graph of g ^-1.  The points (-4,-1), (-2,0), (0,1), (3,2), and (5,4) all lie on the graph of y = g(x) thus the points (-1,-4), (0,-2), (1,0), (2,3), and (4,5) all lie on the graph of y = g ^-1(x).  The graph is shown below.

Problem 2

Let

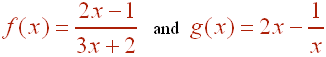
A.  Find gof(1)

Solution

First find f(1).  Plugging in 1 for x gives

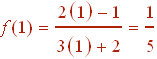
Next plug 1/5 into g, that is, find g(1/5).

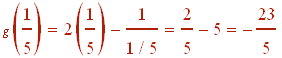
B.  Find and simplify fog(x)

Solution

We find

Now multiply through and then multiply the numerator and denominator by x to get

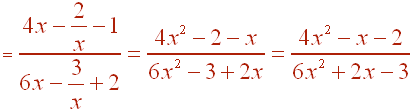
C.  Find f ^-1(x)

Solution

Switch the x's and the y's to get

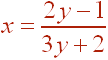
Now solve for y by first multiplying by the denominator:

Next get the y's to the left hand side and the other terms to the right hand side.

Now factor out the y.

Finally, divide by 3x - 2 to get

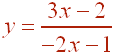
Problem 3

Graph the following.  Then find the domain, range, and asymptote.

A. 

Solution

This has the shape of the y = 2^x graph, but there is a shift and a reflection.  Instead of the graph having y-intercept at (0,1) the graph is shifted to the right by 3, reflected across the horizontal axis, and moved up 1.  Thus the corresponding point is at (3,0).  The point corresponding to (1,2) is at (4,-1).  The new asymptote is the line y = 1 and is still a right asymptote.  The domain stays the same and is all real numbers, but the new range is all real numbers that lie below the asymptote since the reflection is across the horizontal line.  Thus the range is all real numbers from negative infinity to 1, not including 1.  The graph is shown below.

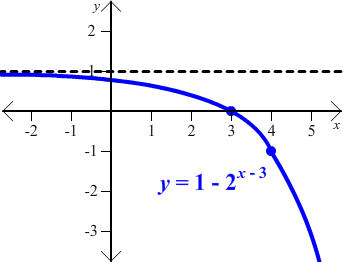
B. 

Solution

We can rewrite this as

f(x)  =  ln(-(x - 2))

Which has the same shape as the graph of y = ln(x) but is shifted to the right by 2 and then reflected across the vertical.  This asymptote will be at x = 2.  Notice that the usual point (1,0) shifts to the point (3,0) and then is reflected across the line x = 2 to arrive back at the point (1,0).  The point (e,1) moves to the point (2-e,1).  The domain is also shifted and reflected.  It will, now lie to the left of the asymptote instead of to the right.  Thus the domain is all numbers from negative infinity to 2 not including 2.  The range is still all real numbers.  The graph is shown below.

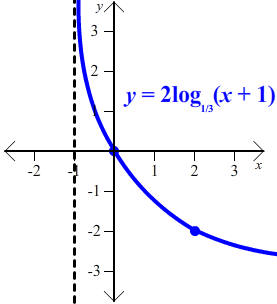
C. 

Solution

This has the same shape as the graph of y = log_1/3(x), which by the change of base formula is the same as y = log₃(x) / log₃(1/3)  =  -log₃(x).  Thus it is the same as the graph of y = log₃(x) but is reflected across the x-axis, shifted to the left by 1 and stretched by a factor of 2.   The graph is shifted to the left by 1 and stretched by a factor of 2.  The vertical asymptote is at x = -1.  The point (1,0) gets transformed to the point (0,0) and the point (3,-1) gets transformed to the point (2,-2).  The graph is shown below.

Problem 4

Solve the following equations

A.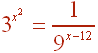 

Solution

Notice that

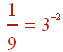
Substituting gives

Now use the fact that the exponential is 1-1 to remove the base 3 to get

x² = -2x + 24

or

x² + 2x - 24  =  0

Factor to get

(x + 6)(x - 4)  =  0

so that

x = -6     or     x = 4

B. 

Solution

Write in exponential form to get

x² = 9

Since the base of a log must be positive, we only include the positive square root or

x = 3

C. 

Solution

First put the logs together

Now use the log rule that allows us to bring a factor up as an exponent

Next, use the log rule that changes subtraction outside the logs to division inside

Next change to exponential form

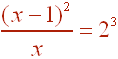
Next cube and multiply by x.

(x - 1)²  =  8x

FOIL:

x² - 2x + 1  =  8x

Set the equation equal to 0 to get

x² - 10x + 1  =  0

Finally, use the quadratic formula to get

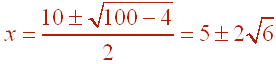
Notice that for the solution to be in the domain, x - 1 must be positive.  This is only true for

D. 

Solution

Take ln of both sides

ln(5^x-1)  =  ln(3^2x)

Now use the log rule for exponents

(x-1) ln5  =  2x ln3

Multiply through

x ln5 - ln5  =  2x ln3

Bring the x terms together

x ln5 - 2x ln3  =  ln5

Factor out an x.

x (ln5 - 2 ln3) =  ln5

Divide to get the final answer

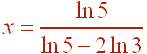
Problem 5

A.  Change the exponential statement to an equivalent statement involving a logarithm.

Solution

"Run the hook"

x  =  log₅(6)

B.  Change the logarithmic statement to an equivalent statement involving an exponent.

Solution

"Run the hook" and recall that ln is base e.

e^x  =  7

Problem 6

Let ln(3) = a  and ln(6) = b.  Write the following in terms of a and b.

A.  ln(2)

Solution

We can write

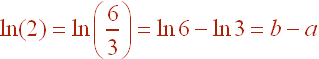
B.  ln(54)

Solution

We can write

C. 

We can write

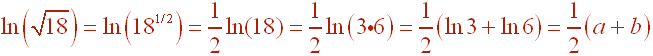
Problem 7

Write the expression as a sum or difference of logarithms. Express powers as factors and simplify all numbers.

Solution

We expand the log remembering that factors that come from the numerator are added and those coming from the denominator are subtracted.

Now use the exponent rule for logs.  Remember that the cube root is the same as the 1/3 power.  Also remember that log100 = 2.

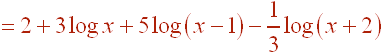
Problem 8

This year, it costs the average family $1000 per month for health insurance.  If the inflation rate is 9% per year (compounded continuously), how long will it take until the cost of health insurance is $1500 per month?

Solution

Use the compound interest formula

A  =  Pe^rt

with

A  =  1500,     P  =  1000,     r  =  0.09

Now plug in to get

1500  =  1000 e^0.09t

Divide by 1000 to get

1.5  =  e^0.09t

Now turn this into logarithmic form

ln 1.5  =  0.09t

Finally divide by 0.09 and put it into a calculator to get

We can conclude that it in approximately four and a half years health care will cost the average family $1500 per month.

Problem 9

A loan company offers a $5,000 loan where the customer makes no monthly payments, but must pay back $7,000 in four years.  Assuming a monthly compounding period, what is the annual interest on this loan?

Solution

We use the compound interest formula

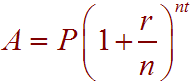
With

A  =  7000,     P  =  5000,     t  =  4,     n  =  12

Now plug in to get

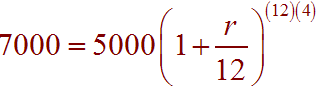
Divide by 5000

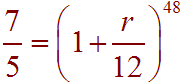
Next, take the 48^th root of both sides, which is the same as taking both sides to the 1/48 power

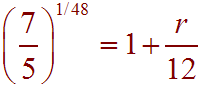
Next, subtract 1, multiply by 12, and put into a calculator to get

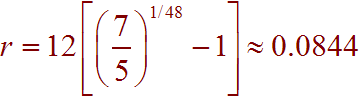
We can conclude that the interest rate is 8.44%.

Problem 10

A culture of bacteria obeys the law of uninhibited growth.  At noon, there were 200 bacteria present and at 1:00 PM there were 250 present.

A.  How many bacteria will be present at 3:00 PM?

Solution

The law of uninhibited growth implies the exponential equation

With

t  =  1  (1:00 PM is 1 hour after noon),     N₀  =  200,     N(1)  =  250

Gives

250  =  200 e^k(1)

Divide by 200 to get

1.25  =  e^k

Turn this into logarithmic form to get

k  =  ln(1.25)

The equation becomes

B.  What is the doubling time for this bacteria?

Solution

The doubling time is the time it takes for there to be twice as much bacteria as there was at the start.  Since the initial amount of bacteria was 200, we want to fine the time when there are 400 bacteria present.  This gives

400  =  200 e^{ln(1.25) t}

Divide by 200 to get

 2  =  e^{ln(1.25) t}

Turn this into a logarithmic equation

ln 2  =  ln(1.25) t

Divide by ln(1.25) and put this into a calculator to get that t is about 3.1 hours.  If we want the time, convert 0.11 hours to minutes by multiplying by 60 to get 6.6 or about 7 minutes.  We can conclude that the doubling time is about 3 hours and 7 minutes.

Problem 11

The half-life of radioactive Cobalt-60 is 5.27 years.  If a terrorist detonates a Cobalt-60 bomb, ground zero will remain uninhabitable until only 2% of the Cobalt-60 remains.  How long will it be until ground zero becomes inhabitable?

Solution

Radioactive decay follows the exponential law

A(t) = A₀ e^kt

The half-live is 5.27 years, that means that when t = 5.27, A is half of what we started with or A = 1/2 A₀.  So that

1/2 A₀  =  A₀ e^k(5.27)

1/2  =  e^k(5.27)

Next put this into logarithmic form

5.27k  =  ln(1/2)

Now divide by 5.27 and put it into a calculator to get that k is approximately equal to -0.1315.  We want to know the time when there is 2% of the original amount.  This gives

0.02 A₀  =  A₀ e^-0.1315t

Divide by A₀ to get

0.02  =  e^-0.1315t

Put this into logarithmic form

-0.1315 t  =  ln(0.02)

Divide by -0.1315 and put the answer into a calculator to get that t is approximately equal to 30.  We can conclude that the ground-zero area will not be inhabitable for approximately 30 years.

Problem 12

A victim whose body temperature before she was murdered was 98.6 degrees Fahrenheit.  The temperature of the room that she was murdered in has been a constant temperature of 65 degrees Fahrenheit since the time of death.  At 3:00 PM the body was found to have a temperature of 80 degrees Fahrenheit.  At 4:00 PM the body had a temperature of 70 degrees Fahrenheit.  What was the time of death?

Solution

We can use Newton's Law of Cooling which is

u(t)  =  T + (u₀ - T)e^kt

with

u₀  =  98.6    and     T  =  65 

We can let 3:00 be s hours after the time of death.  Then 4:00 is s + 1 hours after the time of death.  These give

80  =  65 + (98.6 - 65)e^ks

and

70  =  65 + (98.6 - 65)e^k(s+1)

For both of these equations we can subtract 65 and divide by (98.6 - 65) to get

e^ks  =  0.4464

and

e^k(s+1)  =  0.1488

Now put each of these into logarithmic form to get

ks  =  ln(0.4464)  =  -0.8065

and

k(s + 1)  =  ln(0.1488)  =  -1.905

Multiply the k  through in the second equation to get

ks + k  =  -1.905

so that

ks  =  -k  - 1.905

Set the first ks equation equal to the second to get

-0.8056  =  -k - 1.905

Now solve for k to get

k  =  -1.1

Finally, we can substitute to get

(-1.1)s  =  -0.8065

or

s  =  0.7

Multiply by 60 to put this into minutes to get that the time of death was about 42 minutes before 3:00 PM or at about 2:18 PM.

Problem 13

 The world population P(t) (in billions) t years since 1900 is given by

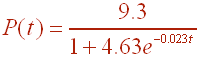
A.  What is the carrying capacity and the rate of growth?

Solution

The exponential part goes to 0 as t goes to infinity, so the carrying capacity is 9.3 billion people.

B.  What was the population in 1900?

Solution

Plug 0 in for t to get that the population was 9.3/5.63 which is about equal to 1.65 billion people.

C.  What was the population in 2010?

Solution

Since 2010 is 110 years after 1900, plug in 110 for t to get that the population in 2010 was about 6.8 billion people

D.  When will the population reach 9 billion?

Solution

We are given the population and want to find the year.  Thus P = 9.  This gives

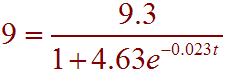
multiply by the denominator to get

9 + 41.67e^-0.023t  =  9.3

Now subtract 9 from both sides and divide by 41.67 to get

e^-0.023t  = 0.0072

Put this into logarithmic form to get

-0.023t  =  ln(0.0072)  =  -4.93

Divide by -0.023 to get

t  =  214

Add this to 1900 to conclude that the population of the earth will reach 9 billion people in the year 2114.