Name
MATH 105 FINAL
Please work out each of the given
problems. Credit will be based on
the steps that you show towards the final answer.
Show your work.
PROBLEM 1 Please answer the following true or false. If false, explain why or provide a counter example. If true, explain why.
A) If
f(x) is a differentiable function that passes through the origin
such that f '(x) > 2
for all x,
then
f(5) cannot equal 10.
Solution
B) If
f(x) is a continuous function such that f
'(0) = 2, f '(1) = 0, and
f '(2) = -3 then f(x)
has a relative maximum at x
= 1.
Solution
C) Suppose that h(x) = g '(x) and that f(x) and h(x) are continuous. Then if g(a) = g(b) ,
![]()
PROBLEM 2 Find the derivative of
A.
f(x) = x cos(x2)
Solution
B.
x2 - 1
f(x)
=
x2 + 1
PROBLEM 3 Find the limit if it exist
![]()
PROBLEM 4 Evaluate the following integrals.
A)
![]()
Solution
B)
![]()
PROBLEM 5 (35 Points) You have a camera that rotates automatically positioned 400m from the space shuttle launch pad. When the space shuttle is 300m from the ground the shuttle is moving at 20 meters per second. How fast should your camera rotate at that instant?
PROBLEM 6 (35 Points) Use right sums with n = 200 to approximate the area under the curve y = 2x + 1, above the x-axis between x = 4 and x = 10.
PROBLEM 7 (35 Points) Let
![]() Find F '(x).
Find F '(x).
PROBLEM 8 (35 Points) Use the limit definition of the derivative to find the derivative of
f(x) = x2 - 2x
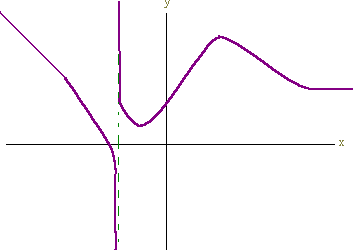
PROBLEM 9 Let
1
f(x) =
1 - x2
Determine any relative extrema, inflection points, intervals where y = f(x) is increasing, intervals where y = f(x) is concave up, and any asymptotes. Then use this information (not you calculator!) to graph the function.
PROBLEM 10
Below is the graph of y = f(x) . Sketch the graph of y = f '(x).