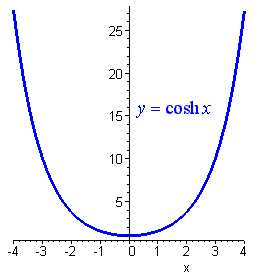
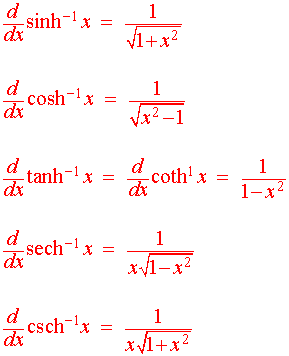Hyperbolic Functions

Definition of the Hyperbolic Functions

We define the hyperbolic functions as follows: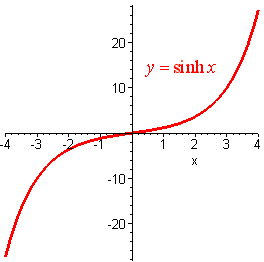

 

ex - e-x      sinh x =                                             2                       ex + e-x      cosh x =                                             2                         sinh x      tanh x =                                      cosh x

Properties

1. (cosh x)² - (sinh x)² = 1 
   

2. d/dx(sinh x) = cosh x
   

3. d/dx(cosh x) = sinh x

Proof of A

We find

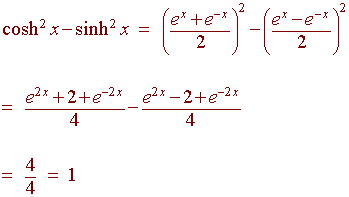
The Derivative of the Inverse Hyperbolic Trig Functions

 

Theorem

Proof of the third identity


We have

        tanh(arctanh x)  =  x

Taking derivatives implicitly, we have

                                   d                                            
       sech²(arctanh x)          arctanh x  =  1
                                  dx                                 

Dividing gives

          d                                             1
                 arctanh x       =                                     
         dx                                 sech²(arctanh x)

Since 

        cosh²(x) - sinh²(x) = 1

dividing by cosh²(x), we get

        1 - tanh²(x) = sech²(x)

so that

          d                                       1                           1
                 arctanh x  =                                   =                 
         dx                         1 - tanh²(arctanh x)          1 - x²

For the derivative of the inverse sech(x) click here

Integration and Hyperbolic Functions

Now we are ready to use the arc hyperbolic functions for integration

Example:  

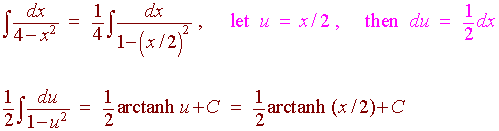
Example

Evaluate

   


Solution

Although this is not directly a derivative of a hyperbolic trig function, we can use the substitution

         u = x² ,    du = 2x dx

To change the integral to

Back to Math 105 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions