Derivative of sech^-1(x)

We use the fact from the definition of the inverse that 

    sech(sech^-1(x))  =  x

and the fact that 

    sech'(x)  =  -tanh(x)sech(x)

Now take the derivative of both sides (using the chain rule on the left hand side) to get

    -tanh(sech^-1x)sech(sech^-1(x))(sech^-1(x))'  =  1

or

  **      -x tanh(sech^-1x)(sech^-1(x))'  =  1

We know that 

        cosh²(x) - sinh²(x)  =  1

Dividing by the cosh²(x) gives

        1 - tanh²(x)  =  sech²(x)

or 

so that 

Finally substituting into **  gives

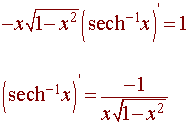
Back to the Page on Hyperbolic Trig

Back to Math 105 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions