Differential Equations

Verifying a Solution to a Differential Equation

The final few pages of this class will be devoted to an introduction to differential equation.  A differential equation is an equation (you will see an "=" sign) that has derivatives.  Some examples are

        y' + 3xy = sin x        and        x²y'' + 3xy' + 4y  =  0

They arise when we know of a relationship between how something is changing, how much of that something there is, and how long the process has been going on.  In algebra when we are told to solve, it means get "y" by itself on the left hand side and no "y" terms on the right hand side.  If y = f(x) is a solution to a differential equation, then if we plug "y" into the equation, we get a true statement.  Often, to plug in we need to take derivatives first.

Example

Verify that

        y  =  e^3x

is a solution to the differential equation

        y'' + 2y' - 15y  =  0

Solution

We compute the first two derivatives.

        y'  =  3e^3x         y''  =  9e^3x

Now substitute y, y', and y'' into the differential equation.

        9e^3x + 2(3e^3x ) - 15(e^3x )  =  e^3x (9 + 6 - 15)

        =  e^3x (0)  =  0

Exercise

Verify that

        y  =  C₁e^x + C₂xe^x

is a solution to the differential equation

        y'' - 2y' + y  =  0

Particular Solutions

In the exercise above, we saw that the general solution involved constants.  The graph below shows the solution for several choices for the solutions.

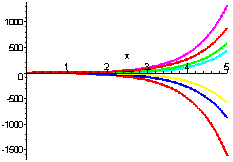
Often, we are given an initial value or values that will assist us to find the constants.

Example

The exercise above stated that

        y  =  C₁e^x + C₂xe^x

is a solution to the differential equation

        y'' - 2y' + y  =  0

If

        y(0) = 2        and        y'(0)  =  3

find the particular solution

Solution

We plug in 0 for t and set y to 2.

        2  =  C₁e⁰ + C₂(0)e⁰ =  C₁

Hence

        y  =  2e^x + C₂xe^x

Now take a derivative to get

        y'  =  2e^x + C₂(e^x + xe^x)

Plug in 0 for t and 3 for y' to get

        3  =  2e⁰ + C₂(e⁰ + (0)e⁰)  =  2 + C₂

so that

        C₂  =  1

The particular solution is

        y  =  2e^x + xe^x

Exercise

Find the particular solution to

        y'' + 4y  =  0         y(0)  =  4        y(p/3)  =  1

Given that

        y  =  C₁sin(2t) + C₂ cos(2t)

Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions