3 Dimensional Coordinates

Definitions

To generalize the plane to 3 dimensions, we draw a third axis, called the z-axis at a right angle from the plane so that if you grab on to the z-axis with your right hand your hand will curl from the positive x-axis to the positive y-axis.  To plot a point in the xyz-space We first plot a point in the xy-plane and then draw a segment parallel to the z-axis of length equal to the z coordinate. 

Example

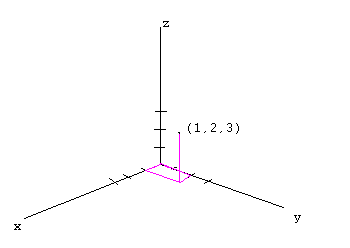
Plot (1,2,3) 

Solution
We first draw the x,y, and z-axes.  Then we plot the point (1,2) in the xy-plane.  Finally move up three units and plot the point.
                       

Exercise

Plot  (2,4,3)

The Distance Formula

The picture below shows how the Pythagorean Theorem relates to distance in three dimensions.  Notice that there are two right triangles.  

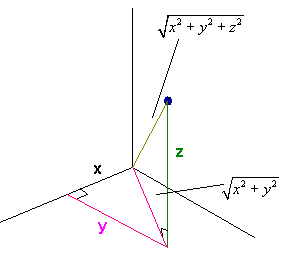
In general, distance between two points (x₁,y₁,z₁) and (x₂,y₂,z₂) and is given by the following

        

Distance Formula in Three Dimensions

Notice that this is just an extension of the Pythagorean Theorem.

Example

Find the distance between the points

    (2,3,10) and (6,2,2)

Solution

We find

        (6 - 2)² + (3 - 2)² + (2-10)²  

        =  4² + 1² + (-8)⁸  =  16 + 1 + 64  =  81

Now take a square root and the distance is 9.

The Midpoint Formula

To find the midpoint of two points (x₁,y₁,z₁) and (x₂,y₂,z₂), we just find the average of each of the coordinates.

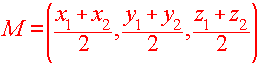
Example

You begin your journey along a straight path at the point (2,-3,5).  When you arrive at the point (3,6,2) you are half way to your destination.  What is the location of your destination?

Solution

We write

        2 + x                    -3 + y                      5 + z
                     =  3,                      =  6,                         =  2  
           2                           2                             2          

        2 + x  =  6,        -3 + y  =  12,        5 + z  =  4

        x  =  4,        y  =  15,        z  =  -1

Our destination is at (4,15,-1).

The Equation of a Sphere

Just as the equation of a circle follows from the distance formula, so does the equation of a sphere.  Since a sphere is defined by the set of all points a distance from a fixed point (h,k,l), squaring the distance formula gives

        (x - h)² + (y - k)² + (z - l)²  =  r²

Here we are using the letter r, for radius, to designate this distance.

Example

The points (5,3,4) and (-1,3,-4) lie on opposite sides of a sphere.  Find the equation of the sphere.

Solution

We need to find the coordinates of the center of the sphere and the radius of the sphere.  The center is the midpoint of the two given point.  We write

         5 - 1           3 + 3            4 + (-4)
                   ,                   ,                          
           2                 2                   2          

Hence the center is at the point (2,3,0).

Now, the distance from the center to a point on the circle is the radius of the circle.  We use the distance formula.

        ^{r2  =  (2 - 5)2 + (3 - 3)2 + (0 - 4)2}

        ^{=  (-3)2 + 02 + (-4)2  =  9 + 16  =  25.}

Putting this all together gives the equation of the circle

        (x - 2)² + (y - 3)² + z²  =  r² 

Traces of Surfaces

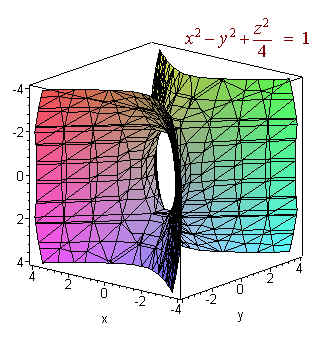
Sketching a surface is quite a challenge.  One way of visualizing a surface is to look at the intersections of the surface with the xy, xz, and yz planes.  These are called the traces of the surface.

Sketch the traces of the surface

Solution

If we let z  =  0, we get

        x² - y²  =  1

This is a hyperbola as shown below

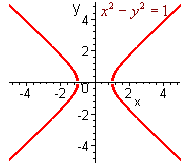
If we let y  =  0, we get the ellipse

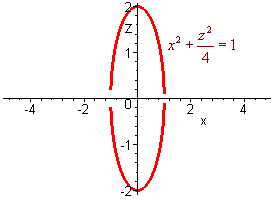
and finally, if we let x  =  0, we get the hyperbola

Since sketching the surface by hand is difficult, we have used a computer to show the three dimensional picture.

Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions