Surfaces

Planes

Just as lines are the simplest and most important curves, planes are the most important surfaces.  The general plane has equation

        ax + by + cz  =  d

To graph a plane with all positive coefficients, we just plot the three points where the plane intersects the axes and connect the dots.  

Example

Graph

        2x + 3y + 4z  =  12

Solution

We first set y and z equal to 0 to get the point

        (6,0,0)

Similarly, we find the other two intercepts 

        (0,4,0)    and    (0,0,3)

Now plot the three points and connect the dots as shown in the picture below.

Quadric Surfaces

In the xy-plane the next step after studying lines is the study of conics:  parabolas, ellipses, and hyperbolae.  Their equations all have x² or y² terms or both.  In three dimensions surfaces whose equations have only linear and quadratic terms are called quadric surfaces.  The naming devise uses the suffix "-oid" to indicate that the surfaces has a trace in the shape of an ellipse.  Note that a circle is a special ellipse.  Below are names of some of these:

•      x²/a² + y²/b² + z²/c² = 1 is an ellipsoid      
  

•     -x²/a²  - y²/b² + z²/c² = 1 is a hyperboloid of 2 sheets while
  

•      x²/a² + y²/b² - z²/c² = 1 is a hyperboloid of 1 sheet
  

•      z  =  x²/a² + y²/b²  is a paraboloid
  

•      z  =  x²/a² - y²/b²  is a hyperbolic paraboloid
  

•     x²/a² + y²/b² - z²/c² = 0 is a cone

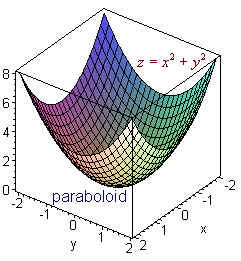
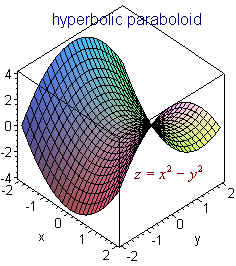
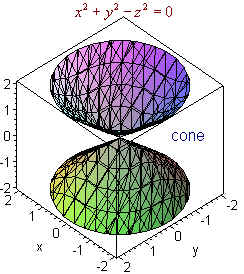
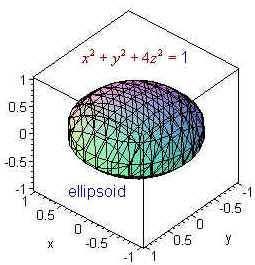
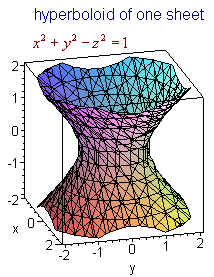
Example

Name the following quadric

Solution

Notice that the trace on the xy-plane is 

        x² - y²  =  1

is a hyperbola and on the xz-plane is

        x² - 4z²  =  1

is also a hyperbola and no the yz-plane is

        x² + 4z²  =  1

is an ellipse.  Since there is only one negative, we see that the surface is a hyperboloid of one sheet.  Its axis is the y-axis. 

Back to the Math 117 Home Page

Back to the Math Department Home

e-mail Questions and Suggestions