Name
MATH 115 MIDTERM III
Please work out each of the given problems.
Credit will be based on the steps that you show towards the final answer.
Show your work.
PROBLEM
1 Without the use of your graphing
calculator,
A)
Determine the relative extrema if
any.
B)
Determine where the function is
increasing and decreasing.
C)
Determine the inflection points if
any.
D)
Determine where the function is
concave up and concave down.
E) Use parts A through D to sketch the graph of the function
I. y = x3 - 12x
We take the first and second derivatives for all four parts:
y' = 3x2 - 12 y'' = 6x
A) Set the first derivative equal to zero.
3x2 - 12 = 0 3x2 = 12 x2 = 4
x = 2 or x = -2
Notice that the function is differentiable everywhere, hence there are no critical points other than 2 and -2.
Now we use the second derivative test for x = -2:
y''(-2) = 6(-2) = -12 < 0
Hence the graph has a relative maximum at x = -2. Plugging into the original equation yields
(-2)3 - 12(-2) = 16
Now we use the second derivative test for x = 2:
y''(2) = 6(2) = 12 > 0
Hence the graph has a relative minimum at x = 2. Plugging into the original equation yields
(2)3 - 12(2) = -16
We conclude that (-2,16) is a relative maximum and (2,-16) is a relative minimum.
B) We want to find out where the first derivative is positive and where it is negative. We draw a number line with the critical points -2 and 2 labeled. We use test points to determine the sign of the first derivative.
y'(-3) = 3(-3)2 - 12 = 15 > 0
y'(0) = 3(0)2 - 12 = -12 < 0
y'(3) = 3(3)2 - 12 = 15 > 0

We can conclude
that the graph is increasing at (-![]() ,
-2) U (2,
,
-2) U (2, ![]() )
)
The graph is decreasing at (-2,2).
C) We set the second derivative equal to zero
6x = 0 x = 0
Plugging into the original equation yields
y = 03 - 12(0) = 0
Hence (0,0) is an inflection point.
D) We determine where the second derivative is positive and where it is negative.
Since the inflection point occurs at x = 0, we use test points on each side of 0.
y''(-1) = 6(-1) = -6 < 0
y''(1) = 6(1) = 6 > 0
![]()
Hence the graph
is concave down on (-![]() ,
0) and concave up on (0,
,
0) and concave up on (0, ![]() ).
).
E) We use the information to sketch the graph.

II. y = 3x4 - 4x3
We take the first and second derivatives for all four parts:
y' = 12x3 - 12x2 y'' = 36x2 - 24x
A) Set the first derivative equal to zero.
12x3 - 12x2 = 0 12x2(x - 1) = 0
x = 0 or x = 1
Notice that the function is differentiable everywhere, hence there are no critical points other than 0 and 1.
Now we use the second derivative test for x = 0:
y''(0) = 36(0)2 - 24(0) = 0
The second derivative test fails, so we need to resort to the first derivative test. We have
y'(-1) = 12(-1)3 - 12(-1)2 = -24 < 0
y'(.5) = 12(.5)3 - 12(.5)2 = -1.5 < 0
The first derivative test tells us that y(0) is neither a relative maximum nor a relative minimum.
Plugging into the original equation yields
3(0)4 - 4(0)3 = 0
The point is (0,0)
Now we use the second derivative test for x = 1:
y''(1) = 36(1)2 - 24(1) = 12 > 0
Hence the graph has a relative minimum at x = 1. Plugging into the original equation yields
3(1)4 - 4(1)3 = -1
We conclude that (0,0) is a horizontal point and (1,-1) is a relative minimum.
B) We want to find out where the first derivative is positive and where it is negative. We draw a number line with the critical points 0 and 1 labeled. We have already found out that y'(-1) < 0 and y'(.5) > 0. We now test
y'(2) = 12(2)3 - 12(2)2 = 24 > 0

We can conclude
that the graph is decreasing on (-![]() ,
0) U (0,1) and is increasing on (1,
,
0) U (0,1) and is increasing on (1, ![]() )
)
C) We set the second derivative equal to zero
36x2 - 24x = 0 12x(3x - 2) = 0
x = 0 or 3x - 2 = 0
x = 0 or x = 2/3
Plugging into the original equation yields
y = 3(0)4 - 4(0)3 = 0
and
y = 3(2/3)4 - 4(2/3)3 = -16/27 = -0.59
Hence (0,0) and (2/3,-0.59) are the inflection points.
D) We determine where the second derivative is positive and where it is negative. We test
y''(-1) = 36(-1)2 - 24(-1) = 60 > 0
y''(.5) = 36(.5)2 - 24(.5) = -3 < 0
y''(-1) = 36(2)2 - 24(2) = 96 > 0

We can conclude that the graph is concave up on (-![]() ,
0) U (2/3,
,
0) U (2/3, ![]() )
and concave down on (0,2/3).
)
and concave down on (0,2/3).
E) The graph is shown below

III.
3x - 4
y =
4x - 3
We take the first and second derivatives for all four parts. We use the quotient rule
(4x - 3)(3) - (3x - 4)(4)
y' =
(4x - 3)2
12x - 9 - 12x + 16
=
( 4x - 3)2
7
=
= 7(4x - 3)-2
( 4x - 3)2
and to find the second derivative, we use the chain rule
u = 4x - 3 u' = 4
f(u) = 7u -2 f '(u) = -14u -3
so
y'' = (4)(-14u -3) = -56(4x - 3)-3
-56
y'' =
(4x - 3)3
A) Since the numerator of the first derivative is a constant, we see that it is never equal to zero. There is a critical point at x = 3/4 which is an asymptote. We can conclude that there are no relative extrema.
B) We want to find out where the first derivative is positive and where it is negative. We draw a number line with the critical point 3/4 labeled. We use test points to determine the sign of the first derivative.
y'(0) = 7(4(0) - 3)-2 = 7/9 > 0
y'(1) = 7(4(1) - 3)-2 = 7 > 0
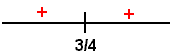
We can conclude that the graph is increasing for all x except at x = -3/4 where there is an asymptote.
C) Since the numerator of the second derivative is a constant, we see that it is never equal to zero. We can conclude that there are no inflection points.
D) We want to find out where the second derivative is positive and where it is negative. Although there are no inflection points, concavity can change at an asymptote. Again, we draw a number line with the critical point 3/4 labeled. We use test points to determine the sign of the second derivative.
y'(0) = -56(4(0) - 3)-3 = -56/27 > 0
y'(1) = -56(4(1) - 3)-3 = 56 < 0
We conclude that the graph is concave up on (-![]() ,
3/4) and concave down on (3/4,
,
3/4) and concave down on (3/4, ![]() ).
).
E) We use the above information to graph the function.

IV.
x
y =
x2 + 1
We take the first and second derivatives for all four parts. We use the quotient rule
(x2 + 1)(1) - (x)(2x)
y' =
(x2 +1)2
x2 + 1 - 2x2
=
(x2 + 1)2
1 - x2
=
= (1 - x2)(x2
+ 1)-2
(x2 + 1)2
and to find the second derivative, we use the product and chain rule
y'' = (1 - x2)[(x2 + 1)-2]' + (-2x)(x2 + 1)-2
u = x2 + 1 u' = 2x
f(u) = u-2 f '(u) = -2u-3
so
y'' = (1 - x2)[-4x(x2 + 1)-3] + (-2x)(x2 + 1)-2
(1 - x2)(-4x)
-2x
=
+
(x2 + 1)3
(x2 + 1)2
4x3 -
4x
-2x (x2 + 1)
=
+
(x2 + 1)3
(x2 + 1)3
2x3 - 6x
=
(x2 + 1)3
A) We set the first derivative equal to zero. This is the same as setting the numerator equal to zero. We have
1 - x2 = 0 (1 + x)(1 - x) = 0
x = -1 or x = 1
Use the second derivative test to find
2(-1)3 - 6(-1)
y''(-1) =
= 1/2 > 0
((-1)2 + 1)3
2(1)3 - 6(1)
y''(1) =
= -1/2 < 0
((1)2 + 1)3
Now plug -1 and 1 back into the original equation to get
1
y(1) =
= 1/2
12 + 1
-1
y(-1) =
= -1/2
(-1)2 + 1
Notice that the denominator of the first derivative is never zero, hence there are no asymptotes. We can conclude that there is a relative maximum at (-1,0.5) and a relative minimum at (1,0.5).
B) We want to find out where the first derivative is positive and where it is negative. We draw a number line with the critical points -1 and 1 labeled. We use test points to determine the sign of the first derivative.
y'(-2) = (1 - (-2)2)((-2)2 + 1)-2 = -3/25 < 0
y'(0) = (1 - (0)2)((0)2 + 1)-2 = 1 > 0
y'(2) = (1 - (2)2)((2)2 + 1)-2 = -3/25 < 0
![]()
Hence
the graph is decreasing on (-![]() ,
-1) U (1,
,
-1) U (1, ![]() )
and it is increasing on (-1,1).
)
and it is increasing on (-1,1).
C) We set the numerator of the second derivative equal to zero. We have
2x3 - 6x = 0 2x(x2 - 3) = 0
x = 0 x = -![]() x =
x = ![]()
We use a calculator to find the y coordinates to get inflection points at
(-1.7,-0.43), (0,0), (1.7,0.43)
D) We have already found the sign of the second derivative at 1 and -1. We test two more points
2(-2)3 - 6(-2)
y''(-2) =
= -4/125 < 0
((-2)2 + 1)3
2(2)3 - 6(2)
y''(2) =
= 4/125 > 0
((2)2 + 1)3
![]()
E) We use the information above to sketch the graph.

PROBLEM
2
You manage the new Spockwood ski resort. Your research shows that if you charge $40
per lift ticket, you can expect to sell 3000
tickets. For every
$5 increase in price you can expect to lose 250 customers.
Assume the demand equation is linear.
A)
Find the demand equation.
Since the demand equation is linear, we need the equation of the line. We find two points:
(3000,40) and (2750,45)
The slope is
45 -
40
5
1
m =
=
= -
2750 -
3000
-250
25
We have
p - 40 = -1/25 (x - 3000) = -1/25 x + 120
so that
p = -1/25 x + 160
B)
What price will yield the maximum revenue?
Recall that revenue is equal to the number of units sold times the price.
R = xp = x (-1/25 x + 80) = -1/25 x2 + 160x
To find the maximum revenue, we take the derivative and set it equal to zero
R' = -2/25 x + 160 = 0
-2x + 4000 = 0
x = 2000
To be certain that this will give a maximum, we take the second derivative
R'' = -2/25
This is always negative, hence it is negative at x = 2000. The second derivative test assures us that this point is a relative maximum.
We plug this into the demand equation to find the price
p = -1/25 (2000) + 160 = 80
The price of $80 will yield the maximum revenue.
C)
Is the demand elastic or inelastic when the price is $45?
p/x
h
=
dp/dx
First find x when p = 45. We have
45 = -1/25 x +120 1/25 x = 75
x = 1875
45 / 1875
h(45)
=
= - .6
-1/25
Since the absolute value of this quantity is less than 1, we can conclude that the demand is inelastic.
PROBLEM
3 At the blood bank, a
cylindrical bottle without top is to contain 100 cc
of blood. What should the
dimensions of the bottle be in order to minimize material costs?
Assume that the glass has the same thickness throughout.
We want to minimize the surface area. The surface area of the bottom (a circle) is
SAb = pr2
and the surface area of the rounded side is
SAs = 2prh
So that the total surface area is
SA = pr2 + 2prh
The volume is given by
V = 100 = pr2 h
so that
100
h =
pr2
Substituting into the surface area equation gives
100
SA = pr2 + 2pr
pr2
200
SA = pr2
+
r
We want to minimize the surface area, hence we take a derivative and set it equal to zero
200
SA' = 2pr -
= 0
r2
2pr3 - 200 = 0 2pr3 = 200 r3 = 100/p
taking a cube root gives that r is approximately 3.17. Notice that if we take a second derivative we get
400
SA'' = 2p +
r3
Which is positive for r = 3.17. Hence this critical point yields a minimum as required. We now find the value of h. We have
100
h =
= 3.17
p(3.17)2
We construct the flask with a radius of 3.17 cm and a height of 3.17 cm.
PROBLEM 4 The department of fish and game have introduced a species of trout that was once native to the region. The number (in hundreds) of this species t years after their introduction can be modeled by the equation
90(2 + 5t)
P(t) =
1 + 10t
Use differentials to approximate the change in the trout population from three
to 3.5 years after their introduction.
We have
DP @ dp/dt Dt
Use the quotient rule to get the derivative
(1
+ 10t)(450) - 90(2 + 5t)(10)
P'(t) =
(1 + 10t)2
Now plug in in t = 3.5 to get
(1 + 10(3))(450) -
90(2 + 5(3))(10)
P'(3.5) =
=
-1.4
(
1 + 10(3))2
We also have Dt = 0.5 so that
DP @ dp/dt Dt = -1.4(0.5) = -0.7
During this half year, the population decreases by approximately 70 fish.