Math 115 Practice Final

Please workout each of the given problems.  Credit will be based on the steps that you show towards the final answer.  Show your work.

 

Problem 1  Find y' for the following

A.  y  =  x2 (1 - x)5

Solution

We use the product rule first

        y'  =  x2 [(1 - x)5]' + (2x)(1 - x)5

Now use the chain rule

        u  =  1 - x        u'  =  -1

        f(u)  =   u5        f '(u)  =  5u4  =  5(1 - x)4 

Now substitute to get

        y'  =  x2(-1)5(1 - x)4  + (2x)(1 - x)5 

        =  -5x2(1 - x)4  + (2x)(1 - x)5 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B. 

Solution

We first change the roots to exponents

        y  =  (x + (2x)1/2)1/2  =  (x + 21/2x1/2)1/2

Now use the chain rule to get

        u  =  x + 21/2x1/2        u'  =  1 + 21/2(1/2 x -1/2)

        f(u)  =  u1/2        f '(u)  =  1/2 u-1/2  =  1/2( x + 21/2x1/2)-1/2

so that

        y'  =  (1 + 21/2(1/2 x -1/2))(1/2( x + 21/2x1/2)-1/2)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C.  x3 - 3xy  =  2    at (2,1)

Solution

We implicitly differentiate, remembering to use the product rule for 3xy.  We have

        3x2 - 3xy' - 3y  =  0

Now plug in 2 for x and 1 for y

        3(2)2 - 3(2)y' - 3(1)  =  0

        12 - 6y' - 3  =  0         9 - 6y'  =  0

        6y'  =  9        y'  =  9/6  =  3/2

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 2  Find the following limits if they exist

A. 

Solution

We plug in to get

            (-1)2 - 4             -3
                               =          
            (-1)2 + 4             5

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B. 

Solution

This time, when we plug in we get

                 (5)2 - 25                   0
                                          =          
            2(5)2 - 9(5) - 5              0

Thus we will need to do some algebra first.  We have

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

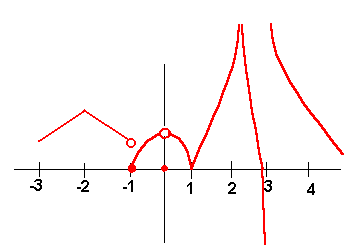
Problem 3  The graph of f(x) is given below.  Find the values of c such that 

A.  does not exist.

Solution

 

The limit does not exist where the left and right hand sides do not meet or give asymptotes. This occurs for 

        x  =  -1, 2, 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B.  f(x) is not continuous at x  =  c.

Solution  

The function is not continuous where either the limit does not exist or there is a hole.  From part A. we get -1, 2, 3.  In addition, there is a hole at x  =  0.  Hence the function is not continuous at 

        x  =  -1, 0, 2, 3

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C.  f(x) is not differentiable at x  =  c.

Solution

The function is not differentiable where it is not continuous and where the tangent line on the left hand side has different slope from the tangent line on the right hand side.  This will occur where the graph is "V" shaped.  The function is not continuous at x  =  -1, 0, 2, 3.  There is not tangent line at x  =  -2, 1.  Hence the function is not differentiable at 

        x  =  -2, -1, 0,1,  2, 3

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 4  The annual revenue of the Tahoe Eats restaurant is pictured in the figure below.  Visually locate the point of inflection.  Interpret this point in terms of how revenue is increasing or decreasing.  What can you say about the revenue growth of the restaurant over the last thirty years?

       

 

Solution

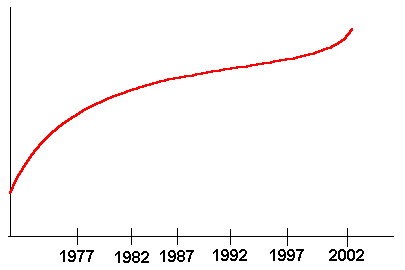
The point of inflection occurs at approximately 1990.  The revenue has been increasing consistently over the past thirty years.  The growth increased rapidly until around 1977 when it slowed down until about 2001, when it again began increasing rapidly.  The year of the slowest growth was around 1990. 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 5  The concentration C in milligrams per milliliter of a chemical in a patient's bloodstream t hours after injection into a muscle tissue is modeled by

                           3t3
        C  =                                          
                    10 - 10t2 + 9t3

A.  Use differentials to approximate the change in concentration of the chemical when t changes from 1 to 1.1 hour.

Solution

We find the first derivative

                    (10 - 10t2 + 9t3)9t2 - 3t3(-20t + 27t2)
        C  =                                                                              
                                   (10 - 10t2 + 9t3)2 

Plug in t  =  1 to get

        

                    ( 10 - 10 + 9)9 - 3(-20 + 27)              60
        C  =                                                         =               @  0.74    
                                   ( 10 - 10 + 9)2                      81

Now use the differential formula

        dC  =  C' dt  =  (0.74)(1.1 - 1)  =  0.074

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B.  Use your graphing calculator to sketch the graph of the concentration and determine how long it will take until the medicine has the greatest effect.

Solution

The graph is shown below

       

From the graph, it looks like it will take approximately 1.7 hours until maximum concentration is reached.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

C.  Find the horizontal asymptote of the concentration function.  If you were a doctor discussing this medication with your patient, how would you explain the medical implications of the horizontal asymptote?

Solution

We find

       

We would explain that for the rest of your life the residual concentration of the medicine in your bloodstream will be 1/3.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 6  Without the use of the graphing capabilities of your graphing calculator, determine the relative extrema, inflection points, and asymptotes.  Determine the relative extrema, inflection points, and asymptotes.  Determine the intervals where the graph of the function is increasing and where it is decreasing.  Determine where the graph is concave up and where the graph is concave down.  Then sketch the graph of the function.  

        y  =  3x4 - 8x3 + 6x2 

Solution

We find the first two derivatives

        y'  =  12x3 - 24x2 + 12x

and

        y''  =  36x2 - 48x + 12

Notice that since the function is a polynomial, there are no asymptotes.  To find the relative extrema, we set the first derivative equal to zero

        12x3 - 24x2 + 12x  =  0        12x(x2 - 2x + 1)  =  0

        12x(x - 1)2  =  0

        x  =  0        or         x  =  1

Plug these values into the original equation to get the points

        (0,0)        and        (1,1)

Now use the second derivative test to classify these points

        y''(0)  =  12

so that (0,0) is a relative minimum

        y''(1)  =  0

We need to use the first derivative test for this critical point.  While we are at it we will check for increasing and decreasing intervals.  We plug the test points -1, 1/2, and 2 into the first derivative to get negative, positive, and positive.  

       

The first derivative test tells us that (1,1) is neither a relative maximum nor a minimum, but rather a stationary point.  The function is decreasing on (- , 0) and is increasing on (0,1) and (1, ).  Next we test for concavity.  We set the second derivative equal to zero

        y''  =  36x2 - 48x + 12  =  0        12(3x2 - 4x + 1)  =  0

        12(3x - 1)(x - 1)  =  0

        x  =  1/3    or     x  =  1

Plugging these into the original equation gives the inflection points.  We get

        (.33, .4)    and     (1,1)

Now use test points to determine concavity.  We test -1, 2/3, and 2.  To get positive, negative, and positive.

               

The graph is concave up in the intervals (-, 1/3) and (1, ) and concave down on (1/3,1).  We can use all this information to graph this curve.  The graph is shown below.

       

        

       

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Problem 7  The demand function for a haircut is 

        x  =  600 - 2p2 

A.  At what price should a haircut be in order to maximize revenue?

Solution

The revenue is the price times number of units sold.

        R  =  xp  =  (600 - 2p2)p  =  600p - 2p3 

To maximize the revenue, we take the derivative and set it equal to zero

        R'  =  600 - 6p2  =  0

        6p2  =  600        p2  =  100        p  =  10

Now take the second derivative to ensure that this gives a maximum.

        R''  =  -12p

which is negative for p  =  10.  By the second derivative test 10 gives a maximum.  The price of a haircut should be $10 in order to maximize revenue.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

B.  Determine the elasticity at the price of $12 and interpret your result.

Solution

  We compute 

                       p/x
         h =                  
                     dp/dx

First find x when p  =  12.  We have

        x  =  600 - 2(12)2  =  312

                          12 / 312
      h(12)  =                             =  - .0008    
                           -4(12)

Since the absolute value of this quantity is less than 1, we can conclude that the demand is inelastic.