The Second Derivative Test

 

II.  Concavity and inflection Points

Example:  Consider a typical ski slope.  At what point on the slope are you having the most fun?  In other words where is the slope the greatest?  

 

We begin with a definition.

 

Definition Of Concavity

 If f '(x) is increasing then the function is concave up and if f '(x) is decreasing then the function is concave down.  

 

Graphically a curve is concave up if it can hold water and concave down if it looks like and upside down cup.  To determine whether the derivative is increasing, we take the second derivative.  

 

Example

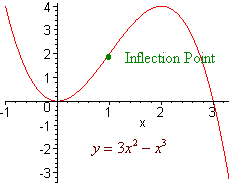
Let 

        f(x)  =  3x2 - x3

Then  

        f '(x)  =  6x - 3x2         and         f ''(x)  =  6 - 6x

Solving 

        6- 6x  >  0

we see that the function is concave up when x <1

Solving 

        6- 6x  <  0

we see that the function is concave down when x > 1

When  x  =  1 we say that f(x) has an inflection point.  

Below is a sketch of f(x)

            

 

Exercise 

Determine where the function is concave up and concave down.  Hold your mouse over the yellow rectangle for the answer.

A)  y  =  x3 - x        concave down for x < 0 concave up for x > 0

B)  y  =  x4 - 6x2         concave up for x < -1 and x > 1 concave down for -1 < x < 1

C)           concave up for all x > -1

 

 

The Second Derivative Test

 

The next theorem states that at a relative maximum the curve is concave down, and for a relative minimum, the curve is concave up.  If a point is a relative maximum then by the first derivative test, the slope to the left is positive and the slope to the right is negative.  Since the slope decreases from positive values to negative values, the first derivative is decreasing.  Hence the second derivative is increasing.  A similar argument holds for a relative minimum.  

 

Theorem  (The Second Derivative Test)

Let f be a twice differentiable function near c such that f '(c) = 0.  Then

1)  If f ''(x) > 0 then f(c) is a relative minimum

2)  If f ''(x) < 0 then f(c) is a relative maximum

3)  If f ''(x) = 0 then use the first derivative test.

 

 

 

Example

Let 

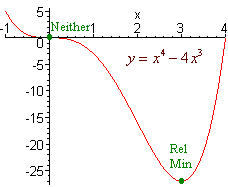
        f(x)  =  x4 - 4x3

Then 

        f '(x)  =  4x3 - 12x2   

which is zero at     x = 0     and     x = 3

        f ''(x) = 12x2 - 24x

        f ''(0) = 0      and     f ''(3) > 0

Hence at x = 3 there is a relative minimum.  At x = 0 we use the first derivative test.  

To the left of 0:     f '(x) < 0

To the right of 0:     f '(x) <0 

thus at x = 0 there is no local extrema.

The graph is pictured below

           

 

 

Exercises

Locate and classify the relative extrema for the following.  Hold your mouse over the yellow rectangle for the answer.

f(x) = 5 + 3x2 - x3    Rel Min at x = 0 Rel Max at x = 2

f(x)  =  x4 - 4x3 + 2    Rel Min at x = 3 Neither at x = 0

f(x) =   x + 4/x    Rel Min at x = 2 Rel Max at x = -2

 

 

Application

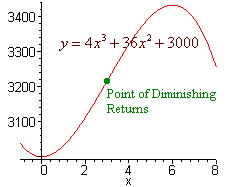
In economics, the inflection point of the profit or revenue functions is called the point of diminishing returns.  Before the inflection point the rate of profit is increasing, while after it is decreasing.  The inflection point is the point where it begins to get more difficult to increase profit.  

 

Example

Find the point of diminishing returns for the function

        R(x)  =  -4x3 + 36x2 + 3000

 

Solution

We take two derivatives

        R '(x)  =  -12x2 + 72x

        R ''(x)  =  -24x + 72

Setting the second derivative equal to zero gives

        -24x + 72  =  0

        x  =  3 is the point of diminishing returns.

The graph is pictured below

           

 

Back to the calculus home page

Back to the math department home page

e-mail Questions and Suggestions