The Dot and Cross Product
The Dot Product
|
Definition
v . w = ac + bd |
Notice that the dot product of two vectors is a number and not a vector. For 3 dimensional vectors, we define the dot product similarly:
|
Dot Product in R3 If v = ai + bj + ck and w = di + ej + fk
then
|
Examples:
If
v
= 2i + 4j
and
w
= i + 5j
then
v . w
= (2)(1) + (4)(5) = 22
Exercise
Find the dot product of
2i + j -
k and
i + 2j
The Angle Between Two Vectors
We define the angle theta between two vectors v and
w by the formula
v
. w
cos q
=
||v|| ||w||
so that
|
v . w = ||v|| ||w|| cos q |
Two vectors are called orthogonal if their angle is a right angle.
We
see that angles are orthogonal if and only if
v . w
= 0
Example
To find the angle between
v = 2i + 3j + k
and
w
= 4i + j + 2k
we compute:
![]()
and
![]()
and
v . w
= 8 + 3 + 2 = 13
Hence

Direction Angles
Definition of Direction Cosines
|
Projections and Components Suppose that a car is stopped on a steep hill, and let g be the force of gravity acting on it. We can split the vector g into the component that is pushing the car down the road and the component that is pushing the car onto the road. We define
Definition Let u and v be a vectors. Then u can be broken up into two components, r and s such that r is parallel to v and s is perpendicular to v. r is called the projection of u onto v and s is called the component of u perpendicular to v. |
We see that
||u|| ||v|| ||projvu ||
u . v = ||u|| ||v|| cos q =
||u||
= ||v|| ||projvu ||
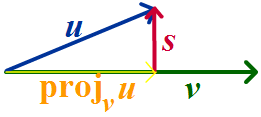
hence
|
u
. v |
We can calculate the projection of u onto v by the formula:
|
u . v |
Notice that this works since if we take magnitudes of both sides we get that
u . v
| |projvu|| =
||v||
||v||2
and the right hand side simplifies to the formula above. The direction is correct since the right hand side of the formula is a constant multiple of v so the projection vector is in the direction of v as required.
To find the vector s, notice from the diagram that
projvu + s = u
so that
s = u - projv u
The work done by a constant force F along PQ is given by
| W = F . PQ |
Example
Find the work done against gravity to move a 10 kg baby from the point (2,3) to the point (5,7)?
Solution
We have that the force vector is
F = ma = (10)(-9.8j) = -98j
and the displacement vector is
v = (5 - 2) i + (7 - 3) j = 3i + 4j
The work is the dot product
W = F . v = (-98j) . (3i + 4j)
= (0)(3) + (-98)(4) = -392
Notice the negative sign verifies that the work is done against gravity. Hence, it takes 392 J of work to move the baby.
Suppose you are skiing and have a terrible fall. Your body spins around
and you ski stays in place (do not try this at home). With proper bindings your bindings will
release and your ski will come off. The bindings recognize that a force
has been applied. This force is called torque. To compute it
we use the cross produce of two vectors which not only gives the torque,
but also produces the direction that is perpendicular to both the force and
the direction of the leg.
The Cross Product Between Two Vectors
|
Definition
|
We can compute this determinant as

= (bf - ce)
i + (cd - af) j +
(ae - bd) k
Example
Find the cross product u x v if
u = 2i + j - 3k v = 4j + 5k
Solution
We calculate

= 17i - 10j + 8k
If you need more help see the lecture notes for Math 103 B on matrices.
Exercises
Find u x v when
-
u = 3i + j - 2k, v = i - k
-
u = 2i - 4j - k, v = 3i - j + 2k
Notice that since switching the order of two rows of a determinant changes
the sign of the determinant, we have
u x v =
-v x u
Geometry and the Cross Product
Let u and v be vectors and consider the parallelogram that
the two vectors make. Then
||u x v|| = Area of the Parallelogram
and the direction of u x v is a right angle to the parallelogram
that follows the right hand rule
Note: For i x j the magnitude is 1 and the direction is k, hence i x j = k.
Exercise
Find j x k and i x
k
Torque Revisited
We define the torque (or the moment M of a force F about a point
Q) as
|
M = PQ x F |
Example
A 20 inch wrench is at an angle of
30 degrees with
the ground. A force of 40 pounds that makes and angle of
45 degrees
with the wrench turns the wrench. Find the torque.
Solution
We can write the wrench as the vector
20 cos 30 i +
20 sin 30 j = 17.3 i + 10 j
and the force as
-40 cos 75 i - 40 sin 75 j = -10.3
i - 38.6 j
hence, the torque is the magnitude of their cross product:

= -564
inch pounds
To find the volume of the parallelepiped spanned by three vectors u,
v, and w, we find the triple product:
|
Volume = u . (v x w) |
This can be found by computing the determinate of the three vectors:

Example
Find the volume of the parallelepiped spanned by the vectors
u = <1,0,2> v = <0,2,3> w = <0,1,3>
Solution
We find

Back to the Math 107 Home Page
