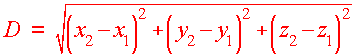Vectors
Directed Line Segments and Vectors
A directed line segment is defined as an initial point,
P, and a terminal
point Q.
Example
P
= (2,3) and Q
= (-1,4)
|
Definition of a Vector A vector is the equivalence class of all directed segments of the same length and direction. |
We can represent a vector by writing the unique directed line segment that
has its initial point at the origin.
Example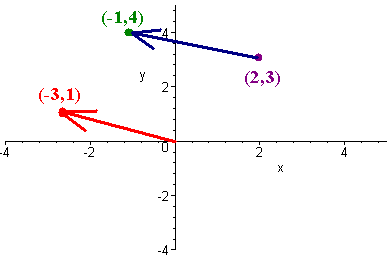
P = (2,3) and
Q = (-1,4)
is
equivalent to the directed line segment
"Q - P"
= <-3, 1>
When we write
the <> we mean that the vector has initial point at the origin and
terminal point at (-3,1). This notation is called the component form
of the vector.
The length of the vector <x,y> is called the norm or magnitude.
We can find it by the formula:
|
Length of a Vector
|
Example:
![]()
We also use the notation
-3i + j
to denote the vector
<-3,1>.
Example
A vector that has length 10 makes an angle of p/6
with the x-axis. Find its components.
Solution:
x = r cos q,
y = r sin q
So that
x = (10)(![]() / 2),
y = 10 (1/2) = 5
/ 2),
y = 10 (1/2) = 5
We can write the vector as
5![]() i + 5j
i + 5j
Unit Vectors in the Direction of v
A vector is called a unit vector if it has
magnitude = 1. If
v = <a,b>
then the unit vector in the direction of v can be found by
|
The Unit Vector in the Direction of v
1
|
Example:
The unit vector in the direction of <-3,1> is
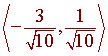
We can use the <> notation and the i
j notation interchangeably.
Algebra of Vectors
If
v = <a,b>
and w = <c,d>
and k is a
constant, then we can define the sum an scalar multiplication as follows
|
Sum and Scalar Multiplication of Vectors
v
+ w = <a + c,b + d> |
Example
3 <2,1> - 2<-1,3> = <6 + 2,3 - 6>
= <8,-3> =
8i
- 3j
Geometrically v + w is the vector that corresponds to the diagonal of the parallelogram with two sides v and w.
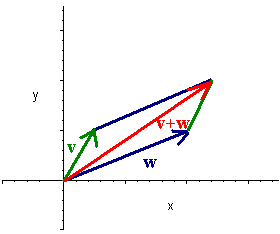
The appropriate diagram can also be drawn to show how
v
- w = v + (-w).
You can see vector addition with this applet.
You can play with other arithmetic of vectors here.
Properties of Vector Addition and Subtraction
We have the following four properties of vectors: If u, v
,and w are vectors and a and
b are numbers then
-
(u + v) + w = u + (v + w)
-
a(u + v) = au + av
-
a(bv) = (ab)v
-
u + v = v + u
Applications
An boat captain wants to travel due south at 40 knots. If the
current is moving northwest at 16 knots, in what direction and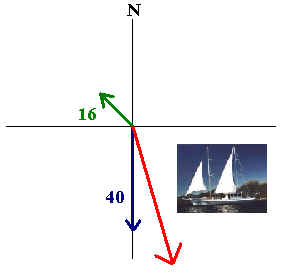 magnitude
should he work the engine?
magnitude
should he work the engine?
Solution
We have
u = v +
w
where u corresponds to the velocity vector of the boat, v
corresponds to the engine's vector, and w corresponds to the velocity
of the current. We have
u = -40j
and w = -8![]() i +
8
i +
8![]() j
j
Hence
v = u - w
= -40j - (-8![]() i + 8
i + 8![]() j)
= 8
j)
= 8![]() i -
(40+8
i -
(40+8![]() )j
)j
The magnitude is
[(8![]() )2
+ (40+8
)2
+ (40+8![]() )2]1/2
= 52.5
)2]1/2
= 52.5
The direction is
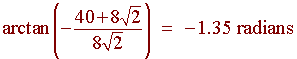
3 Dimensional Coordinates
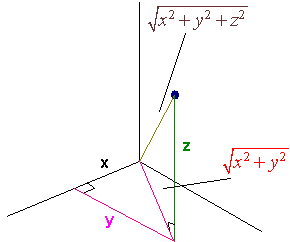
To generalize the plane to 3 dimensions, we draw a third axis, called the z-axis at a right angle from the plane so that if you grab on to the z-axis with your right hand your hand will curl from the positive x-axis to the positive y-axis. To plot a point in the xyz-space We first plot a point in the xy-plane and then draw a segment parallel to the z-axis of length equal to the z coordinate.
Example:
Plot (1,2,3)
Solution:
We first draw the x,y, and z-axes. Then we plot the point (1,2) in the
xy-plane. Finally move up three units and plot the point.
Exercise
Plot (2,4,3)
The Distance Formula
The distance formula is derived from the three dimensional version of the
Pythagorean theorem, which is displayed below.

The distance between two points
(x1,y1,z1) and (x2,y2,z2) and is given by
| Distance Formula
in Three Dimensions
|
Algebra of vectors in 3D
A vector in space is given by
<x,y,z> = xi + yj +
zk
The algebra rules are similar to those in two dimensions.
Back to the Math 107 Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions