Sequences and Series
-
Sequences
Example: Find the next term and describe the pattern:
-
2, 4, 6, 8, 10, ...
-
1, 4, 9, 16, 25, ...
-
3, 7, 15, 31, 63, ...
-
1, -1/2, 1/6, -1/24, 1/120, -1/720, ...
Solution:
-
We see that the next term is 12. We can get to the next term by adding two.
-
The next term is 36. The terms are all squares.
-
The next term is 127. These numbers are all one less than a power of two.
The next term is 1/5040. The numbers alternate sign and the denominators are all factorials.
Definition
A sequence is a list of numbers. In technical terms, a sequence is a function whose domain is the set of natural numbers and whose range is a subset of the real numbers.Example:
Consider the function
f(n) = 2n + 1This function describes the sequence
3,5,7,9,11,...
We will usually use the notation an to describe a sequence instead of the notation f(n).
-
-
Finding the General Element of a Sequence
One technique for finding the general element an is to list the numbers 1,2,3,4,5,6... above the sequence and decide what do we have to do to the number 5 for example to get the fifth term. then generalize.Example
Find the general element an in the exercises listed above.
Solution:-
an = 2n
-
an = n2
-
an = 2n+1 - 1
-
an = (-1)n+1 /n!
-
-
Recursively Defined Sequences
A recursively defined sequence is a sequence where the first term(s) are given and the next term is given in terms of the previous terms.
Example
Let
a1 =1, a2 = 1and
an = an - 1 + an - 2
This is called the Fibonacci sequence and the terms are
1,1,1+1 = 2,1+2 = 3,2+3 = 5,3+5 = 8,5+8 = 13,8+13 = 21,...
1,1,2,3,5,8,13,21,34,55,...
-
Sigma Notation and Series
Definition
We define a series to be the sum of the sequence.Example:
If
1,1/2,1/4,1/8,...
is a sequence, then
1 + 1/2 + 1/4 + 1/8 + ...
is the corresponding sum. We define the nth partial sum as
sn = a1 + a2 + a3 + ... + anWe write this series in Sigma Notation as follows.
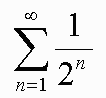
This is read, "The sum from 1 to infinity of 1 over 2 to the n."
Application:
ex = 1 + x + x2/2! x3/3! ... xn/n! + ... =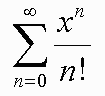
Back to the College Algebra Part II (Math 103B) Site
Back to the LTCC Math Department Page
e-mail Questions and Suggestions