Exponentials
-
Example of an Exponential Function
A biologist grows bacteria in a culture. If initially there were three grams of bacteria, after one day there are six grams of bacteria, and after two days, there are twelve grams, how many grams will there be at the end of the week?
Solution:
We draw a t chart
t P(t) 0 3 = 3(20) 1 6 = 3(21) 2 12 = 3(22)
We see that the general formula isP(t) = 3(2t)
Hence after one week, we calculate
P(7) = 3(27) = 384 grams of bacteria.
We call P(t) and exponential function with base 2.
-
Graphing Exponentials
Below is the graph of y = 2x. It turns out that for any b > 1 the graph of y = bt looks similar.
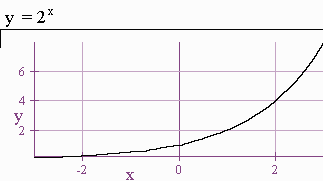
Notice that
-
the left horizontal asymptote at 0
-
The y-intercept is 1
-
The graph is always increasing.
Shifting techniques can also be used to graph variations of this curve.
Example
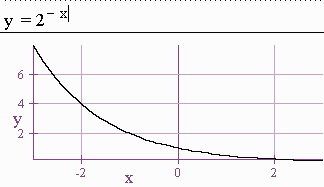
Graph y = 2-x
Solution:
We see that the graph is reflected about the y-axis:
-
-
Three Properties of Exponents
-
bx by = bx+y
-
bx / by = bx-y
-
(bx)y = bxy
Definition
b-x = 1 / bx
ExampleSimplify
34(-3)-1/[(32)3]
Solution34(-3)-1/[(32)3] = 34(-3)-1/ 36
= -34 /(3136) = -34 / 37
= -1/33 = -1/27
-
-
Applications
Money and Compound Interest
We have the formula for compound interest
A = P(1 + r/n)nt
where A corresponds to the amount in the account after t years in a bank that gives an annual interest rate r compounded n times per year.
Example
Suppose we have $2,000 to put into a savings account at a 4% interest rate compounded monthly. How much will be in the account after 2 years?We have
P = 2,000, r = .04, n = 12 and t = 2
We want A.A = 2000(1 + .04/12)12(2) = $2,166.29.
Continuous Interest
For continuously compounded interest, we have the formula:
A = Pert
Inflation Example
With an 8% rate of inflation in the health industry, how much will health insurance cost in 45 years if currently I pay $200 per month?
Solution
We have
r = .08, P = 200, and t = 45
So thatA = 200e(.08)(45) = $7319 per month!
Back to the College Algebra Part II (Math 103B) Site
Back to the LTCC Math Department Page
e-mail Questions and Suggestions