A Comparison of Numerical Integration Applets
There are over a dozen learning objects that all can perform
numerical integration. This webpage attempts to assist the instructor or
student with locating them, rating them and comparing them. For each site,
you can click on the
![]() button to view a popup that gives a description of some of the features and
shortcomings of the applet. A rating
system has been established that looks at layout, functionality, ease of use,
graphical display, on page information, and links to external resources.
The summary can be found in both summative and tabular format by scrolling down towards the bottom
of this page or by clicking on the bookmark links below:
button to view a popup that gives a description of some of the features and
shortcomings of the applet. A rating
system has been established that looks at layout, functionality, ease of use,
graphical display, on page information, and links to external resources.
The summary can be found in both summative and tabular format by scrolling down towards the bottom
of this page or by clicking on the bookmark links below:
Qualitative Comments on Each Site
A Table Rates Different Qualities of the 14 Numerical Methods Applets
Below is a list of all of the Numerical Integration Applets that Reside on MERLOT
- Dave Eck, A Riemann Sums Configurable Applet:
http://math.hws.edu/javamath/config_applets/RiemannSums.html
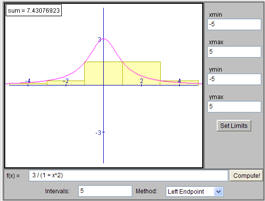

- University of Utah, Finding the Area Under a Curve:
http://www.math.utah.edu/~carlson/teaching/java/calculus/ApproxArea.html
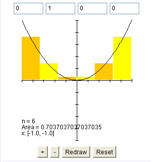

- Thomas E. Leathrum, Numerical Integration:
http://cs.jsu.edu/mcis/faculty/leathrum/Mathlets/trapsimp.html

- Nicholas Exner, Methods for Numerical Integration:
http://www.mste.uiuc.edu/activity/integration/default.html
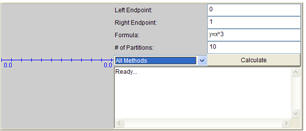

- Thomas Downey, Midpoint and Trapezoidal Riemann Sums:
http://www.calculusapplets.com/midpointtrap.html
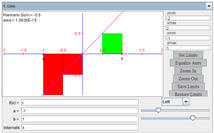

- Donald Kreider and Dwight Lahr, Numerical Integration:
http://math.dartmouth.edu/~klbooksite/appfolder/tools/NumericalIntegration.html
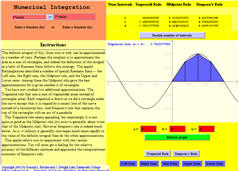

- John Wiley & Sons, Numerical Integration Applet:
http://www.wiley.com/college/mat/anton243310/mod2/applet1/applet1.html
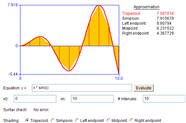

- Peter Maserick, Numerical Integration:
http://www.math.psu.edu/courses/maserick/integration/integ.html
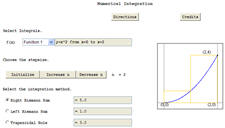

- Dan Sloughter ,Numerical Integration Rules:
http://math.furman.edu/~dcs/java/NumericalIntegration.html

- Joseph Zachary, Numerical Integration Simulation:
http://www2.cs.utah.edu/~zachary/isp/applets/Integrate/Integrate.html

- Ken Levasseur, Riemann Integration:
http://www.hostsrv.com/webmaa/app1/MSP/webm1010/riemann.msp


- Mike May, Riemann Sums:
http://www.slu.edu/classes/maymk/Riemann/Riemann.html

- Miguel Bayona, Riemann Sums:
http://mathplotter.lawrenceville.org/mathplotter/mathPage/riemann.htm

- Scott Sarra, Riemann Sums Applet:
http://www.scottsarra.org/applets/calculus/RiemannSums.html
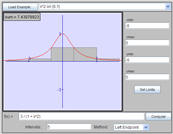

List of Qualitative Comments on Each Site
(Click on the
![]() button to
jump to the icon for this site.)
button to
jump to the icon for this site.)
- The best site for instructors to imbed the applet directly onto their
own web page. No Simpson's Rule or links about the calculus, but very user
friendly.

- This is just a demo of y = x2. Very limited in
functionality.

- Takes a long time to load, Shades the region, but not the approximation.

- Graph very limited. No control of viewing rectangle and no shading
given.

- Very easy to use and graphics including the shading of the approximation
is clear. Gives all approximations except Simpson's. Uses a
slider or input to change a and b.

- Contains all the elementary approximation techniques. The graph is
very responsive and allowing for clear visualization. It took some
time to learn how to resize the viewing rectangle. Click to zoom out
and construct a rectangle with the mouse to zoom in. No external links
given.

- Easy to use, but no internal or external help. Will only work if
students know how to enter in functions. Graphics include shading and
most approximations are provided.

- Very basic and limited to just 4 predefined functions. The
rectangles are outlined but not shaded in. There is a help button, but
nothing to explain the underlying mathematics.

- This only contain a single approximation. The shading does not contain
outlines, so the rectangles or trapezoids are difficult to visualize.

- This applet contain a choice of 12 pre-defined functions. The
screen usually needs to be refreshed for the results to show clearly.
Outlines of the rectangles are given but they are not shaded in. The
menu driven File, Help, Method, and Function choices are easy to navigate.

- Has user input of functions, but there is no help on how to input
functions. Some of the syntax of this input is not natural and it is
not obvious when a mistake is made. This is the only applet that
demonstrates random intervals and random choices of each x-value.

- This one has it all. User input of function, predefined functions,
graphical interface with shading, links for help, all the typical
approximations, and even a worksheet.

- This site uses Geogebra. It contains all the functionality, user
defined functions, sliders that allow for changing the coefficients of the
function and the number of partitions. The endpoints can be dragged.
The only thing missing is the supporting information or links that explain
the calculus.

- This site has predefined functions and user input functions. It is
easy to use and the graphics are straightforward. No Simpson's Rule
capability.

A Table Rates Different Qualities of the 14 Numerical Methods Applets
| GS | CSM | OSSI | EL | UDFV | CADI | LAV | ETII | CO | Overall | |
| 1 | A | B | B | F | A | B | A | A | A | B |
| 2 | B | C | B | F | C | F | F | A | A | C |
| 3 | A | B | A | A | A | F | F | A | A | C |
| 4 | B | A | A | A | A | F | A | A | C | B- |
| 5 | A | B | A | B | A | A | A | B | B | A- |
| 6 | A | B | B | D | D | B | A | A | C | A- |
| 7 | A | C | D | A | A | F | C | A | A | B |
| 8 | B | B | C | F | D | F | B | A | A | C+ |
| 9 | A | A | D | F | D | F | A | A | A | C |
| 10 | A | A | A | C | C | F | B | A | A | C |
| 11 | A | A | B | C | A | F | A | A | A | B |
| 12 | A | A | A | A | A | F | C | B | B | A |
| 13 | A | A | D | C | A | A | A | A | A | A- |
| 14 | B | A | B | F | A | F | A | A | A |
GS = Graphical Support
CSM = Complete Set of Methods
OSSI = On Site Supporting Info
EL = External Links
UDFV = User Defined Functions and Values
CADI = Click and Drag Interface
LAV = Labeled Axes (values)
ETII = Easy to Input Info
CO = Clear Output
Questions Comments Suggestions
Home Pages
e-mail Questions and Suggestions
This work is licensed under a Creative Commons License.