Area and Volume of Complex Objects

In this lesson we will look at finding the area and volume of objects that are created either by putting together simple objects or by cutting out one simple object from another.  It is assumed that you are already familiar with the geometry formulas associated with rectangles, circles, and triangles.  If you need some review of this, go to the lesson on basic shapes.  The strategy that we will take to find the area of these complex objects is the following.

Strategy to Find the Area of Complex Objects

1. Identify whether the object is formed by combining basic shapes or by removing a basic shape from another basic shape.
   
    
2. Find the area of each shape identified in step 1.
   
    
3. Add the areas if the the object is formed by combining these basic shapes or subtract the areas if the object is formed by removing a basic shape from another basic shape.

Example 1

Find the area of the figure shown below

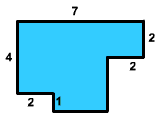
Solution

1. We can realize this as three rectangles glued together.  There is more than one way to do this.  (Note that another approach is to remove two rectangles from a larger rectangle).  Below is one way of cutting this rectangle into three pieces.
   
          
   
    
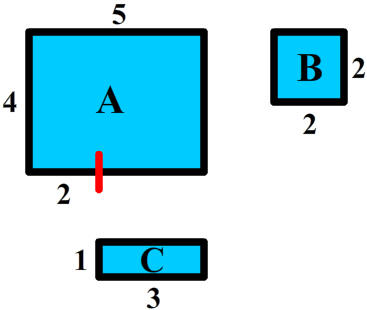
2. Notice that we were able to find the width of rectangle C by seeing that this is the long width of 7 minus the short width of 2 minus another short width of 2:
   
        7 - 2 - 2  =  3
   
   Also notice that the width of rectangle A is 5 since we have cut out the right hand part, "B", of length 2 from the long side of length 7. 
   
   Now we find the areas of each rectangle.  Recall that the area of a rectangle is the length times the width.
   
       Area of Rectangle A  =  (4)(5)  =  20
   
       Area of Rectangle B  =  (2)(2)  =  4
   
       Area of Rectangle C  =  (1)(3)  =  3
    
3. We add up the three areas to find the total area.
   
       Total Area = Area of A + Area of B + Area of C
   
                        =  20 + 4 + 3  =  27
   
   So  the total area is 27 square units.

Now try one by yourself.  If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.

Exercise 1

Find the area of the region shown below.  (Hint:  The area of a right triangle with base b and height h is A  =  1/2 bh).

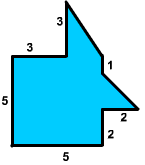
Answer

Example 2

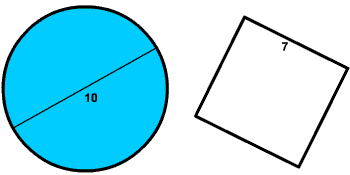
A square with side length 7 is inside in a circle of diameter 10.  Find the area of the part of the circle that does not contain the square.

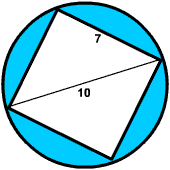
Solution

1. Notice that we are "taking a square away from a circle."  The diagram below shows the two figures sketched separately.
   
          
    
2. Now we find the area of the two regions.  The formula for the area of a circle is 
   
           Area of a Circle  =  pr²  ≈  3.14 r²
   
   We are not given the radius directly, but we are given the diameter.  Recall that the radius is half of the denominator.
   
           r  =  (1/2)(10)  =  5
   
   this gives us
   
           Area of the Circle  =  3.14(25) 
   
                                        =  (3.14)(25)
   
                                        =  78.5
   
   Te find the area of the square, we just square the side length
   
           Area of Square  =  7²  =  49
    
3. Finally, we are ready to find the area of the shaded in region.  This area is the area of the circle minus the area of the square.
   
           Total Area  =  Area of the Circle - Area of the Square
   
                             =  78.5 - 49  =  29.5

Now try one by yourself.  If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.

Exercise 2

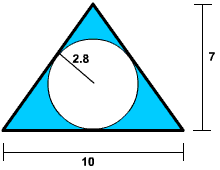
A circle of radius 2.8 is removed from the triangle shown below.  Find the remaining area.  (Round your answer to one decimal place.

Answer

Volume

We will use a similar strategy to find volumes of three dimensional shapes.  Here are the steps to find such volumes.

Steps for finding the volume of complex solids

1. Identify the pieces that the solid is made out of. 
   
    
2. Find the volume of each piece.
   
    
3. Add the volumes together to get the total volume.

Example 3

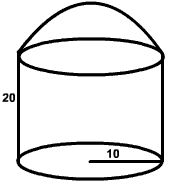
A building is constructed by topping a cylindrical can with height 20 feet and base radius 10 feet with a hemispherical solid as shown in the figure below.  Find the approximate volume of this building.  Recall that the volume of a hemisphere is A = 2/3 p r³ and the volume of a cylinder is A = p r²h.  Use 3.14 for p and 0.67 for 2/3.  Round your answer to the nearest whole number.

Solution

1. Notice that this solid is composed of a cylinder and a hemisphere.
   
    
2. The volume of the cylinder is
   
           Volume of the cylinder      =  p r²h
   
                                                  ≈ 3.14 (10)²(20)
   
                                                  =  3.14(100)(20)
    
                                                  =  (314)(20)
   
                                                  =  6280
   
         Volume of the hemisphere   =  2/3 p r³

                                                       ≈ (0.67)(3.14) (10³)

                                                       =  (0.67)(3.14)(1000)

                                                       ≈  2104

3. Now add the two volumes to arrive at the total volume.
   
           Total Volume  =  Volume of the cylinder + Volume of the hemisphere
   
                                  =  6280 + 2104
   
                                  =  8384
   
   The total volume is 8384 cubic feet.

Now try one by yourself.  If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.

Exercise 3

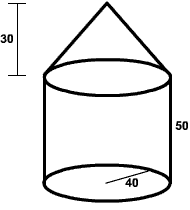
A tower is formed by attaching a cone of height 30 feet onto a cylinder that has radius 40 feet and height 50 feet as shown below.  Find the volume of the tower.  The volume of a cone is
 
    Volume of Cone  =  1/3 p r²h

and the volume of a cylinder is

    Volume of Cylinder  =  p r²h 

Use 3.14 for p and round your answer to the nearest whole number.

Answer

Surface Area

There are many different types of surface area problems.  We will focus on finding the surface area when the solid is composed of cubes that all have the same side length.  To solve such a surface area problem, find the area of the top and bottom, left and right, and front and back.  Then add the areas to get the total area.

Example 4

One inch cubes are stacked as shown in the drawing below.  What is the total surface area?

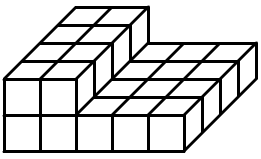
Solution

We will first find the area of the top and the bottom.  Notice that these areas are the same.  Looking at the top from above (or the bottom from below), we can see that this is just a rectangle.

The rectangle has base 5 and height 4.  The area is

        Area of Top  =  (5)(4)  =  20

The area of the bottom is also 20.

Now let's find the area of the left and right side.  Looking from the right, we also see a rectangle.  The rectangle's base is 4 and height is 2. 

Its area is

        Area of Left Side  =  (4)(2)  =  8

The area of the right side is also 8.

Next we find the area of the front.  To find this area, we can just count the squares.  There are 7 squares. 

        Area of the Front  =  7

the area of the back is the same as the area of the front.  That is, the area of the back is also 7.  We could have also arrive at an area of 7 by cutting the figure into two rectangles and adding the areas of these rectangles.

To find the total area, we add up the areas of all of the sides.

        Total Surface Area  =  20 + 20 + 8 + 8 + 7 + 7 

                                       =  70

The total surface area is 70 square inches.

Exercise 4

One inch cubes are stacked as shown in the drawing below.  What is the total surface area?

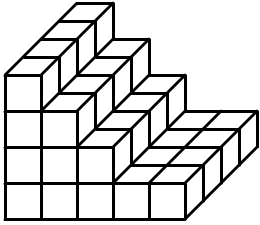
Answer