Figures in the Coordinate Plane
In this lesson, we will review the coordinate plane and plotting points in the plane. We will explore translations and reflections of 2-dimensional figures. Finally, we will use the coordinate plane to find the dimensions and area of two dimensional figures.

The diagram pictured above is called the coordinate plane. The horizontal line labeled "x" is called the x-axis and the vertical line labeled "y" is called the y-axis. The point that is plotted has coordinates (1,3) since the point is 1 unit to the right and 3 units above the origin (the point where the x-axis and y-axis meet). A point is reflected across the x-axis if its x-coordinate stays the same and its y-coordinate is multiplied by -1. Graphically, we can think of a reflection across the x-axis as moving it to its mirror image where the mirror is the x-axis. Similarly, a point is reflected across the y-axis if its y-coordinate stays the same and its x-coordinate is multiplied by -1. Graphically, we can think of a reflection across the y-axis as moving it to its mirror image where the mirror is the y-axis. If we pick up a point and move it, we say that we are translating the point. We can also pick up a 2-dimensional object and move it. We say that we are translating the object.
Example 1
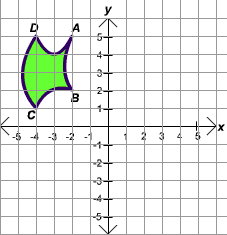
The front side of a pendant is shown below.
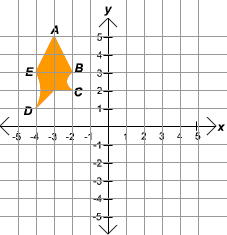
- If the back side of the pendant will be drawn by reflecting the drawing
across the x-axis, what will be the coordinates of
D after the reflection?
- If the back side of the pendant will be drawn by reflecting the drawing
across the y-axis, what will be the coordinates of
A after the reflection?
Solutions
- Since we are reflecting across the x-axis, the x-coordinate
stays the same and the y-coordinate is multiplied by
-1. The coordinates of point
D are (-4,1),
so the coordinates of D reflected across
the x-axis are (-4,-1). Notice
that multiplying a number by -1 is the same as
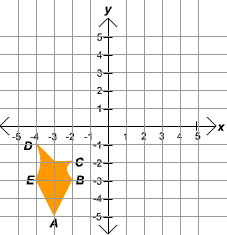
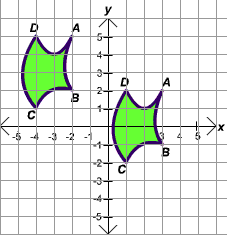
changing the sign of the number. It is a good idea to sketch a drawing
of the reflected region and make sure that the coordinates match the
coordinates of the point on the reflected diagram. The sketch of the
reflected diagram is shown below. Notice that the new point
D does have coordinates
(-4,-1).
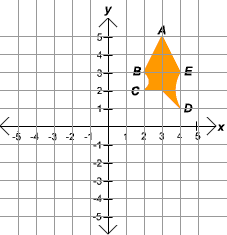
- Since we are reflecting across the y-axis, the y-coordinate
stays the same and the x-coordinate is multiplied by
-1. The coordinates of point
A are (-3,5),
so the coordinates of A reflected across
the y-axis are (3,5). The sketch of the
reflected diagram is shown below. Notice that the new point
A does have coordinates
(3,5).
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
Exercise 1
What are the coordinates the image of B when the triangle ABC is reflected across the x-axis?
![]()
Example 2
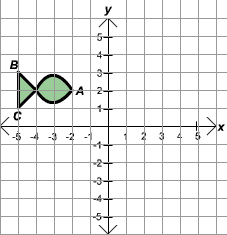
A T-shirt print is to be made by taking the pattern below and including a second pattern that is 5 units to the right and 3 units below the first pattern. What will the new coordinates of point C be?
Solution
Before translation, the point C has coordinates (-4,1). Since we are moving the point 5 units to the right, the new x-coordinate is
x = -4 + 5
= 1
and since we are moving the point 3 units down, the new y-coordinate is
y = 1 - 3
= -2
So the new coordinates of the point C are (1,-2).
The sketch of the translated pattern is shown below. We can see that C does have coordinates (1,-2).
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
Exercise 2
Margarita wants to sketch two fish that are the same shape. She has already drawn one fish shown below. The second fish is to be drawn 2 units above and 4 units to the right of the first fish. What will be the coordinates of the new point A?
![]()
The CAHSEE often tests to see if you remember the names of the common polygons. Recall that a polygon is a closed shape bounded only by straight lines. Here are some of these definitions.
- Triangle: A
polygon with
3 sides

- Quadrilateral:
A polygon with
4 sides

- Rectangle: A
quadrilateral whose angles are all right angles

- Rhombus: A
quadrilateral whose sides all have the same length

- Parallelogram:
A quadrilateral whose opposite sides are parallel. Notice that a
rhombus is also a parallelogram.

- Trapezoid: A
quadrilateral with two parallel sides

- Pentagon: A
polygon with
5 sides

- Hexagon: A
polygon with
6 sides
Example 3
The points (2,1), (4,1), (5,4), and (1,4) are the vertices of a polygon. What type of polygon is formed by these points?
Solution
First sketch the points on the xy-plane. Then connect the points to form the polygon. The sketch is shown below.
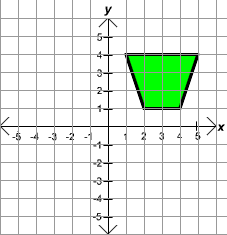
Since the figure has 4 sides, it is not a triangle, pentagon, or a hexagon. The left and right sides are not parallel so it is not a parallelogram. The top and bottom sides have different lengths, so it is not a rhombus or a square. The angles are not right angles, so is it not a rectangle. Notice that the top and bottom are parallel, so this is a trapezoid.
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
Exercise 3
The points (1,1), (3,1), (4,6), and (2,6) are the vertices of a polygon. What type of polygon is formed by these points?
A. Triangle
B. Trapezoid
C. Parallelogram
D. Pentagon
![]()
Another use of the coordinate plane is to find the lengths and area of the given geometric shape.
Example 4
The graph of the square ABCD is shown below. What is the length of one of the sides of this square?
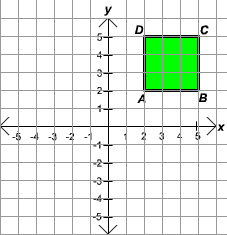
Solution
Since ABCD is a square, all sides have the same length. We will find the distance from A to B. Counting, we see that B is exactly 3 units to the right of A. The length of the sides of the square are all 3 units.
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
Exercise 4
The graph of the equilateral triangle ABC is shown below. What is the length of one of the sides of this equilateral triangle?
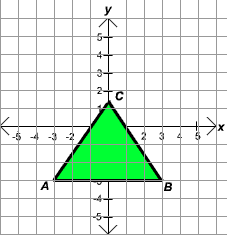
![]()
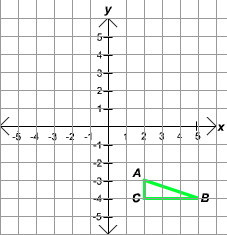
Example 5
The graph of the right triangle ABC is shown below.
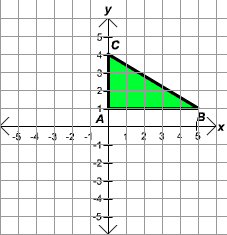
Find the area of this triangle in square units.
Solution
We use the formula for the area of a right triangle.
Area = 1/2 bh
where b is the length of the base of the triangle and h is the height of the triangle. The length of the base is the distance from A to B. We measure this as
b = 5 units
The height is the distance from A to C. We measure this as
h = 3 units
So that
Area = (1/2)(5)(3)
= 15/2
= 7.5
The area of the triangle is 7.5 square units.
Now try one by yourself. If you want to see the answer, put your mouse on the yellow rectangle and the answer will appear.
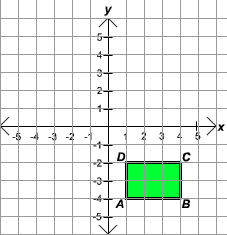
Exercise 5
The graph of the rectangle ABCD is shown below. What is the area in square units of this rectangle?
![]()