Series Solutions to Second Order Linear Differential Equations
We have fully investigated solving second order linear differential equations with constant coefficients. Now we will explore how to find solutions to second order linear differential equations whose coefficients are not necessarily constant. Let
P(x)y'' + Q(x)y' + R(x)y = g(x)
Be a second order differential equation with P, Q, R, and g all continuous. Then x0 is a singular point if P(x0) = 0, but Q and R do not both vanish at x0. Otherwise we say that x0 is an ordinary point. For now, we will investigate only ordinary points.
Example
Find a solution to
y'' + xy' + y = 0 y(0) = 0 y'(0) = 1
Solution
Since the differential equation has non-constant coefficients, we cannot assume that a solution is in the form y = ert. Instead, we use the fact that the second order linear differential equation must have a unique solution. We can express this unique solution as a power series
![]()
If we can determine the an for all n, then we know the solution. Fortunately, we can easily take derivatives
![]()
Now we plug these into the original differential equation
![]()
We can multiply the x into the second term to get
![]()
We would like to combine like terms, but there are two problems. The first is the powers of x do not match and the second is that the summations begin in differently. We will first deal with the powers of x. We shift the index of the first summation by letting
u = n - 2 n = u + 2
We arrive at
![]()
Since u is a dummy variable, we can call it n instead to get
![]()
Next we deal with the second issue. The second summation begins at 1 while the first and third begin at 0. We deal with this by pulling out the 0th term. We plug in 0 into the first and third series to get
(0 + 2)(0 + 1)a0+2x0 = 2a2
and
a0x0 = a0
We can write the series as
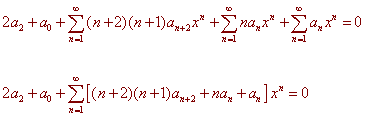
The initial conditions give us that
a0 = 0 and a1 = 1
Now we equate coefficients. The terms in the series begin with the first power of x, hence the constant term gives us
2a2 + a0 = 0
Since a0 = 0, so is a2. Now the coefficient in front of xn is zero for all n. We have
(n + 2)(n + 1)an+2 + (n + 1)an = 0
Solving for an+2 gives
-an
an+2
=
n+2
We immediately see that
an = 0
for n even. Now compute the odd an
-1
1
-1
a1 =
1 a3 =
a5 =
a7 =
3
3.5
3.5.7
In general
(-1)n
2n(n!)(-1)n
a2n+1
=
=
3.5.7.....(2n+1)
(2n + 1)!
The final solution is
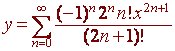
This cannot be written in terms of elementary functions, however a computer can graph or calculate a value with as many decimal places as needed.
Example
Find the the first three nonzero terms of two linearly independent solutions to
xy'' + 2y = 0
Solution
Notice that 0 is a singular point of this differential equation. We will not be able to find a solution in the form Sanyn, since the solution will not be differentiable at zero. Alternatively, we find a solution in the form
![]()
This is the power series centered about x = 1, which is not a singular point. Now take derivatives
![]()
Plugging into the differential equation gives
![]()
Writing
x = (x - 1) + 1
and multiplying through gives
![]()
Let u = n - 2 in the first summation, u = n - 2 in the second and then changing the index variable back to n gives
![]()
Now plugging in n = 0 into the second and third series we get
![]()
Now we can equate coefficients to find
2a2 + 2a0 = 0
(n + 1)nan+1 + (n + 2)(n + 1)an+2 + 2an = 0
The first equation says that
a2 = -a0
The recursion relationship says
-(n + 1)nan+1 - 2an
an+2
=
(n + 2)(n + 1)
We want to find two linearly independent solutions. To do this, we can choose the first two terms of the series. The easiest choices are
a0 = 0 a1 = 1 and a0 = 1 a1 = 0
Plugging the first pair, we get
a0 = 0 a1 = 1 a2 = 0 a3 = [-2(0) - 2(1)]/6 = -1/3
a4 = [-2(3)(-1/3) - 2(0)]/12 = 1/6
Plugging in the second pair, we get
a0 = 1 a1 = 0 a2 = -1 a3 = [-2(-1) - 2(0)]/6 = 1/3
We can write
y1 = (x - 1) - 1/3 (x - 1)3 + 1/6 (x - 1)4 + ...
y2 = 1 - (x - 1)2 + 1/3 (x - 1)3 + ...
Click here for an additional example
Back to the Power Series Methods and Laplace Transforms Home Page
Back to the Differential Equations Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions