Modeling with First Order Differential Equations

Modeling with First Order Differential Equations

Whenever there is a process to be investigated, a mathematical model becomes a possibility. Since most processes involve something changing, derivatives come into play resulting in a differential equation. We will investigate examples of how differential equations can model such processes.

Example A Polluted Pond

A pond initially contains 500,000 gallons of unpolluted water has an outlet that releases 10,000 gallons of water per day. A stream flows into the pond at 12,000 gallons per day containing water with a concentration of 2 grams per gallon of a pollutant. Find a differential equation that models this process and determine what the concentration of pollutant will be after 10 days.

Solution

We let x(t) be amount of pollutant in grams in the pond after t days.

We use a fundament property of rates:

Total Rate = Rate In - Rate Out

To find the rate in we use

             grams                gallons      grams              12,000      2
                             =                                      =
              day                     day         gallon                  1           1

= 24,000 grams per day

To find the rate out we first notice that since there was initially 500,000 gallons of water in the lake and the water level is increasing at a rate of 2,000 gallons per day, the total number of gallons of water in the lake after t days is

gallons = 500,000 + 2,000 t

The units for the rate out is grams per day. We write

             grams                gallons      grams              10,000                 x
                             =                                      =
              day                     day         gallon                  1           500,000 + 2,000 t

                 10x
        =                    grams per day
               500 + 2t

Putting this all together, we get

             dx                                   10x
                         = 24000   -
              dt                                500 + 2t

This is a first order linear differential equation with

                                10
             p(t) =                             g(t) = 24,000
                            500 + 2t

We have

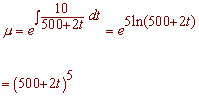
Multiplying by the integrating factor and using the reverse product rule gives

((500 + 2t)⁵x)' = 24,000(500 + 2t)⁵

Now integrate both sides to get

(500 + 2t)⁵x = 2,000(500 + 2t)⁶ + C

                                                          C
            x   = 2000(500 + 2t) +
                                                     (500 + 2t)⁵

Now use the initial condition to get

                                                C
            x   = 2000(500) +
                                             (500)⁵

C = -3.125 x 10¹⁹

Now plug in 10 for t and calculate x

                                                          -3.125 x 10¹⁹
            x   = 2000(500 + 2(10)) +
                                                          (500 + 2(10)⁵

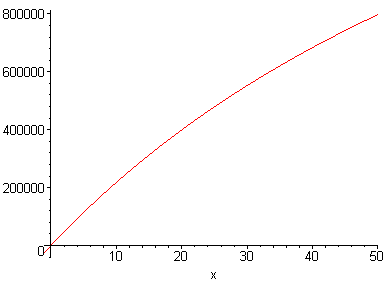
= 218,072 grams

A graph is given below

Example

You just won the lottery. You put your $5,000,000 in winnings into a fund that has a rate of return of 4%. Each year you use $300,000. How much money will you have twenty years from now?

Solution

This is also a

Total Rate = Rate In - Rate Out

problem. Let

x = the balance after t years

The rate out is

300,000

and the rate in is

.04x

We have the differential equation

dx/dt = .04x - 300,000

This is both linear first order and separable. We separate and integrate to obtain