Mechanical and Electrical Vibrations

Consider a mass m  attached to a spring.  We will investigate how the forces on the mass produce a differential equation.  

• By Hook's Law, the spring acts on the mass by 
  
          F_s  =  -ku
  
  Where u is the displacement from equilibrium.
  
  
• Since there are no truly ideal springs, we must consider a damping force which is proportional to the velocity.  That is 
  
          F_d  =  -gu'  
  
• There may be an external force, such as a wind or water current.  
  
          F_e  =  F

Putting these all together and using Newton's law

        F  =  ma  =  mu''

we get

        mu''  =  -ku - gu' + F

or

Undamped Free Vibrations

If there is no external force, and we assume the spring to be an ideal undamped spring, then the differential equation becomes

        mu'' + ku  =  0

Since m and k are both positive, we get the complex roots

       mr² + k  =  0

Which has complex roots with l  =  0  and m²  =  k/m

We call

         w₀²  =  k/m

In particular, the solution for the undamped free spring is 

        u  =  A cos (w₀ t) + B sin (w₀ t)       

This is periodic motion with period

        T  =  2p(m/k)^1/2 

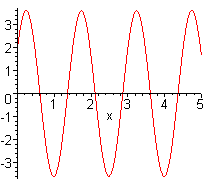
The graph below shows the solution for m  =  4 and k  =  9

Damped Free Motion

If we do not ignore friction, then we get damped free motion.  The equation becomes

        mu'' + gu' + ku  =  0

The characteristic equation is 

        mr'' + gr' + kr  =  0

The solution depends on the sign of g² - 4km.  We have the following three cases

1. g² - 4km  < 0:  The solution is 
   
        u  =  e^-gt/2m (A cos(mt) + B sin(mt))                        4km - g²
                                                                      m²  =                                 
                                                                                          4m²
   
   
2. g² - 4km  = 0:  The solution is 
   
           u  =  (A + Bt)e^-gt/2m 
   
   
3. g² - 4km  > 0:  The solution is 
   
           u  =  Ae^r2t  +  Be^r1t
   
   Where r₁ and r₂ are the real roots of the characteristic equation.  Notice that these roots are both negative since
   
           g² - 4km < g² 

In all three cases u tends to 0 as t tends to infinity. 

When the damping is small compared to km, we are in the first case.  After a change of variables and some trig we end up with 

        u  =  Re^-gt/2m cos(mt - d)

Notice that u is between

        -Re^-gt/2m  <  u  < Re^-gt/2m 

We can say that u is decreasing exponentially in absolute value.  

Below is the graph of damped oscillation. 

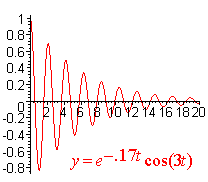
Notice that this is not a periodic function since the amplitude is decreasing (exponentially). We call the length of time between local maximum to local maximum the quasi-period of the function and we call m the quasi-frequency.  We have

        m / w₀  =  (1 - g/4km)^1/2 

Using the binomial series, we get the approximation

        m / w₀  @  1 - g/8km

which is a good approximation when g/8km is small.

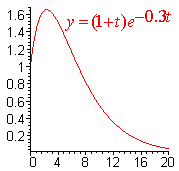
If g² - 4km  = 0, then the motion is called critically damped, and the motion is not periodic.  Below is an example if this.

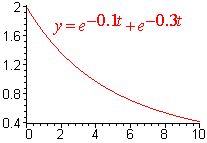
If g² - 4km  > 0, then the motion is called overdamped.  Below is an example if this.

Electrical Circuits

On of the greatest benefits of differential  equation, is that once we know how to solve a differential equation, any physics problem that can be modeled by the differential equation becomes easy.  It turns out that springs and electrical circuits can be modeled by the same differential equation.  Suppose we have an electrical circuit with current I passing through a resistor with resistance R, a capacitor with capacitance C, and in inductor with inductance L.  Let E be the voltage and Q be the charge.  Then there are relationships

        I  =  dQ/dt        V_R  =  IR        V_C  =  Q/C        V_L  =  L dI/dt

Substituting, we get

        L I' + RI + 1/C Q  =  E

and

This is a second order linear differential equation with constant coefficients.  We can solve with the techniques that we have learned.  We can also take the equation with the I's and differentiate to get

which is also a second order linear differential equation with constant coefficients.

Back to the Application and Higher Order Equations Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions