Variation of Parameters for Higher Order Differential Equations

For second order nonhomogeneous differential equations, we saw that if the function g(x) does not generate a UC-Set, then we must use the method of variation of parameters.  To review this method click here.  It turns out that the method of variation of parameters naturally generalizes to higher order differential equations.

Let 

        L(y)  =  y⁽ⁿ⁾ + p₁y^(n-1) + ... + p_n-1y' + p_ny  =  g(t)

and suppose that the general solution to L(y)  =  0  is given by 

        y_h  =  c₁y₁ + c₂y₂ + ... + c_ny_n 

As with variation of parameters for second order equations, we assume that

        y_p  =  u₁y₁ + u₂y₂ + ... + u_ny_n 

where the u_i are functions of t.  Following the prior discussion, we see that we need only one y_p but have labeled n functions of t.  We therefore may impose n - 1 conditions on the u's.  The conditions that we impose are

        u₁y₁' + u₂y₂' + ... + u_ny_n' 

        u₁'y₁' + u₂'y₂' + ... + u_n'y_n' 

        u₁''y₁' + u₂''y₂' + ... + u_n''y_n' 

             |             |                  |

        u₁^(n-1) y₁' + u₂^(n-1) y₂' + ... + u_n^(n-1) y_n' 

Now take derivatives to get

        y_p'  =  u₁y₁' + u₁'y₁ + u₂y₂' +u₂'y₂ + ... + u_ny_n' + u_n'y_n =  u₁'y₁ + u₂'y₂ + ... + u_n'y_n 

        y_p''  =  u₁'y₁' + u₁''y₁ + u₂'y₂' +u₂''y₂ + ... + u_n'y_n' + u_n''y_n =  u₁''y₁ + u₂''y₂ + ... + u_n''y_n 

            |            |            |

        y_p^(n-1)  =   u₁^(n-1)y₁ + u₂^(n-1)y₂ + ... + u_n^(n-1)y_n 

Plugging in to the original differential equation and noting that each of the y's are solution to the differential equation, we get

        y₁^(n-1)u₁' + y₂^(n-1)u₂' + ... + y_n^(n-1)u_n'  =  g(t)

Notice that this gives a system of n equations and n unknowns.  We can write this as

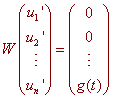
Since the Wronskian is never zero, we can take its inverse.  Taking the inverse of matrix where the entries are functions is not easy.  Fortunately, we only need the last column of the inverse, which can be found with much less pain using the adjoint formula.  

Example

Solve 

        y''' + y'  =  sec t

Solution

We first find the homogeneous solution.  The characteristic equation is 

        r³ + r  =  0

        r(r² + 1)  =  0

        r  =  0,        r  =  i,         r  =  -i

We conclude 

        y_h  =  c₁ + c₂ cos t + c₃ sin t

We have

        y_p  =  v₁ + v₂ cos t + v₃ sin t

and the Wronskian matrix is

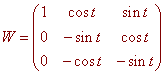
The Wronskian is 

        |W|  =  1(sin² t + cos² t) - cos t (0 - 0) + sin t (0 - 0)  =  1

The matrix equation takes the following form

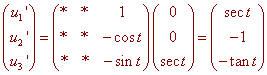
So that 

        u₁'  =  sec t        u₂'  =  -1        u₃'  =  -tan t

Integrating, we get

        u₁'  =  ln|sec t + tan t|       u₂'  =  -t        u₃'  =  ln|cos t|

The final solution is

        y  =  c₁ + c₂ cos t + c₃ sin t + ln|sec t + tan t|  -t cos t + (sin t) ln|cos t|

Back to the Application and Higher Order Equations Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions