Systems with Complex Eigenvalues

In the last section, we found that if 

        x'  =  Ax

is a homogeneous linear system of differential equations, and r is an eigenvalue with eigenvector z, then

        x  =  ze^rt 

is a solution.  (Note that x and z are vectors.)  In this discussion we will consider the case where r is a complex number

        r  =  l + mi

First we know that if r  =  l + mi is a complex eigenvalue with eigenvector z, then 

        r  =  l - mi

the complex conjugate of r is also an eigenvalue with eigenvector z.  We can write the solution as 

        x  =  k₁ze^{(l + mi)t} + k₂ze^{(l - mi)t}

We can use Euler's formula to get

        x  =  k₁ze^lt(cos(mt) + i sin(mt)) + k₂ze^lt(cos(mt) - i sin(mt)) 

Writing

        z  =  a + bi        and        z  =  a - bi

We get

        x  =  k₁(a + bi)e^lt(cos(mt) + i sin(mt)) + k₂(a - bi)e^lt(cos(mt) - i sin(mt)) 

Now multiplying and separating into real and imaginary parts, we get

        x  =  e^lt[k₁(a cos(mt) - b sin(mt)  +  i(a sin(mt) + bcos(mt))) 

                 + k₂(a cos(mt) - b sin(mt) -  i(a sin(mt) + bcos(mt)))]

Now let

        k₁ + k₂  =  2c₁        and         (k₁ - k₂)i  =  2c₂ 

Then we get

        x  =  e^lt[c₁(a cos(mt) - b sin(mt))  +  c₂(a sin(mt) + bcos(mt))]

Example       

        x'  =  -2x + 6y

        y'  =  -3x + 4y

Solution

We have 

To find the eigenvalues, we find the determinant of 

We get 

        (-2 - r)(4 - r) + 18  =  r² - 2r + 10  =  0

The quadratic formula gives the roots

        r  =  1 + 3i        and        r  =  1 - 3i

Now we find and eigenvector corresponding to the eigenvalue 1 + 3i.  Plugging into A - rI, we get

The top row gives

        (-3 - 3i)x  + 6y  =  0

or

        (1 + i)x - 2y  =  0

An eigenvector is 

Hence the general solution is 

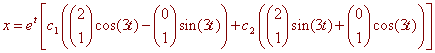
This can be written as

        x  =  e^t[2c₁cos(3t) + 2c₂sin(3t)]

        y  =  e^t[c₁(cos(3t) + sin(3t)) + c₂(sin(3t) + cos(3t))]

Below is the phase portrait

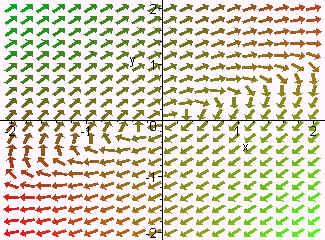
We can see that the solutions spiral out from the origin.  This situation is called a spiral node.  The spiral occurs because of the complex eigenvalues and it goes outward because the real part of the eigenvalue is positive.  If the real part of the eigenvalue had been negative, then the spiral would have been inward.

Back to the Power Series Methods and Laplace Transforms Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions