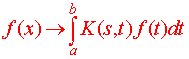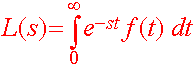The Laplace Transform

The Laplace Transform

We have seen many techniques of solving differential equations that involve using a substitution. There is a special type of substitution, called an integral transform that simplifies the task of solving differential equations.

Definition of an Integral Transform

Let K(s,t) be a function of two variables. The the Integral Transform with Kernel K, is defined as the mapping that takes functions to functions by the rule

Note: a and b can be any real numbers or even infinity or negative infinity

The most important integral transform in the field of differential equations is when a is 0, b is infinity, and K(s,t) is e^-st.

Definition of the Laplace Transform

Let f(x) be a function. Then the Laplace Transform of f(x) is

Example

Find the Laplace Transform of f(x) = x².

Solution

We just work out the integral

This can be worked out by integrating by parts twice.

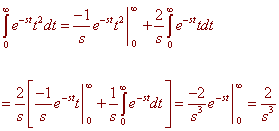
We used the fact that

for all s > 0. This fact is easily proven using induction and LHopital's rule.

We can see that finding the Laplace transform of a function us just a matter of integration. We will usually see integration by parts enter into the picture.

Exercises

Find the Laplace transform of the following functions

A. f(x) = sin(at)

B. f(x) = cos(at)

C. f(x) = e^at

D. f(x) = tⁿ n a positive integer

E. f(x) = e^at sin(bt)

Our next question to ask is when the Laplace transform of a function is defined. Since the Laplace transform of a function is defined as an improper integral, the integral may not converge. Fortunately most of the functions that we know and love have convergent Laplace transforms. More generally we have the following theorem.

Theorem

Let f(t) be a piecewise continuous function on 0 < t < A for any A. Also let

|f(t)| < Ke^at

for all t > M with K, a and M real constants and K and M positive.

Then the Laplace transform L{f(t)} = F(s) exists for s > a

Proof

First, since f(t) is piecewise continuous, for large values of t, f(t) is continuous. Since convergence only depends on the behavior for large values of t, we can assume that f is continuous. To finish the proof we substitute the larger Ke^at for the smaller f(t) to get

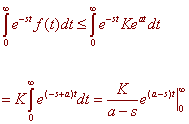
This converges whenever a < s.

Another important fact about Laplace Transforms is that the Laplace transform is a linear transformation from "nice" functions to functions, where "nice" means functions that have a Laplace transform. That is,

L{f(t) + g(t)} = L{f(t)} + L{g(t)}

and

L{cf(t)} = cL{f(t)}

Back to the Power Series Methods and Laplace Transforms Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions