Discontinuous Forcing
In the last section we looked at the Heaviside function its Laplace transform. Now we will use this tool to solve differential equations.
Example
A 1 kg bar is attached to a large spring with spring constant 5 and damping constant 2. It is pulled down 3m from it's equilibrium position and then released. After one second a constant force of 10 Newtons is exerted on the bar. The force remains turned on indefinitely. Determine the equation of motion of the bar.
Solution
We have the differential equation
y'' + 2y' + 5y = 10u1(t) y(0) = 3 y'(0) = 0
We solve this by the method of Laplace transforms. We have
L{y''} + 2L{y'} + 5L{y} = 10L{u1(t)}
s2L{y} - 3s - 0 + 2(sL{y} - 3) + 5L{y} = 10e-s /s
(s2 + 2s + 5)L{y} - 3s - 6 = 10e-s /s
3s +
6
10
L{y}
=
+ e-s
s2 + 2s +
5
s(s2 + 2s + 5)
We use partial fractions on the second term
10
A
Bs + C
=
+
s(s2 + 2s +
4)
s
s2 + 2s + 5
A(s2 + 2s + 5) + (Bs + C)s = 10
(A + B)s2 + (2A + C)s + 5A = 10
The constant term gives
A = 2
Thus
B = -2 C = -4
We can complete the square
s2 + 2s + 5 = (s + 1)2 + 4
Putting all the algebra together we get
3s +
6
2
-2s - 4
L{y}
=
+ e-s
+ e-s
(s + 1)2 + 4
s
(s + 1)2 + 4
s + 1 +
1
2
(s + 1) + 1
= 3
+e-s
- 2e-s
(s + 1)2 + 4
s
(s + 1)2 + 4
s
+1
2
2
s +
1
2
= 3
+ 3/2
+ e-s
- 2e-s
- e-s
(s + 1)2 + 4
(s + 1)2 + 4
s
(s + 1)2 + 4
(s + 1)2 + 4
Now use the table to take the inverse Laplace transform to get
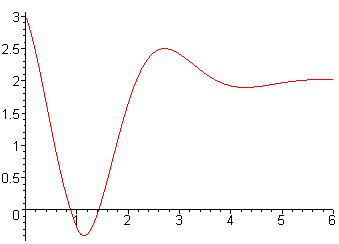
y = 3e-tcos(2t) + 3/2 e-t -1sin(2t) + 2u1 - 2u1(t)e-t +1 cos(2t - 2) - u1(t)e-t +1 sin(2t - 2)
Below is the graph

Back to the Power Series Methods and Laplace Transforms Home Page
Back to the Differential Equations Home Page