Complex Roots of the Characteristic Equation

We have already addressed how to solve a second order linear homogeneous differential equation with constant coefficients where the roots of the characteristic equation are real and distinct.  We will now explain how to handle these differential equations when the roots are complex.  The example below demonstrates the method.

Example

Solve 

        y'' - 4y' + 13y  =  0

Solution

As before we assume that y  =  e^rt is a solution.  We have

        y'  =  re^rt        y''  =  r²e^rt 

Substituting back into the original differential equation gives

        r²e^rt - 4re^rt + 13e^rt  =  0

        r² - 4r + 13  =  0        dividing by e^rt 

This quadratic does not factor, so we use the quadratic formula and get the roots

        r  =  2 + 3i         and        r  =  2 - 3i

We can conclude that the general solution to the differential equation is

        y  =  a₁e^(2+3i)t + a₂e^(2-3i)t

        =  a₁e^2te^3it + a₂e^2te^-3it      Using the rule of exponents

        =  e^2t(a₁e^3it + a₂e^-3it)     Factoring out the e^2t 

Although this gives the general solution, it it not satisfactory since the solution involves complex exponents.  To deal with this we use Euler's formula

        e^iq  =  cos q + i sin q

This gives 

        y  =  e^2t[a₁(cos(3t) + i sin(3t)) + a₂(cos(-3t) + i sin(-3t))]

Since the cos x is an even function and sin x is an odd function, we get

        y  =  e^2t[a₁(cos(3t) + i sin(3t)) + a₂(cos(3t) - i sin(3t))]

or

        y  =  e^2t[(a₁ + a₂)cos(3t)  + (a₁ - a₂)i sin(3t)]

Finally let 

        c₁  =  a₁ + a₂         and        c₂  =  i(a₁ - a₂)  

and we get 

        y  =  e^2t[c₁cos(3t)  + c₂ sin(3t)]

In general if 

        ay'' + by' + cy  =  0

is a second order linear differential equation with constant coefficients such that the characteristic equation has complex roots

        r  =  l + mi     and    r  =  l - mi

Then the general solution to the differential equation is given by 

        y  =  e^lt[c₁ cos(mt) + c₂sin(mt)]

Example

Solve 

        y'' - 10y' + 29  =  0        y(0)  =  1    y'(0)  =  3

Solution

The characteristic equation is

        r² - 10r + 29  =  0

which has roots 

        r  =  5 + 2i        and        r  =  5 - 2i

The general solution is 

        y  =  e^5t[c₁ cos(2t) + c₂ sin(2t)]

We use the initial values to find the constants.  Plug in y(0)  =  1.

        1  =  1[c₁(1) + c₂(0)]

so that c₁  =  1.  We have

        y'  =  5e^5t[cos(2t) + c₂ sin(2t)] + e^5t[-2 sin(2t) + 2c₂ cos(2t)]

Plugging in y'(0)  =  3

        3  =  5[1 + 0]  + 1[0 + 2c₂]  =  5 + 2c₂ 

Hence c₂  =  -1

The final solution is 

        y  =  e^5t[cos(2t) - sin(2t)]

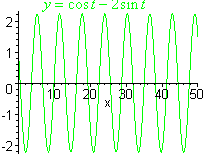
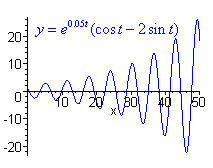
Let's investigate the graphs of solutions of the form

                y  =  e^lt[c₁ cos(mt) + c₂sin(mt)]

For  l  =  0, the graph is periodic.

For l  >  0, the amplitude increases exponentially

For l < 0, the amplitude approaches 0 exponentially.

The three types are pictured below.

Back to the Linear Second Order Differential Equations Home Page

Back to the Differential Equations Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions