Linear Independence and Span

Span

We have seen in the last discussion that the span of vectors v₁, v₂, ... , v_n is the set of linear combinations

        c₁v₁ + c₂v₂ + ... + c_nv_n  

and that this is a vector space.  

We now take this idea further.  If V is a vector space and S  =  {v₁, v₂, ... , v_n) is a subset of V, then is Span(S) equal to V?

Definition

Let V be a vector space and let S  =  {v₁, v₂, ... , v_n) be a subset of V.  We say that S spans V if every vector v in V can be written as a linear combination of vectors in S.

        v  =  c₁v₁ + c₂v₂ + ... + c_nv_n  

Example

Show that the set 

        S =  {(0,1,1), (1,0,1), (1,1,0)} 

spans R³ and write the vector (2,4,8) as a linear combination of vectors in S.

Solution

A vector in R³ has the form 

        v  =  (x, y, z)

Hence we need to show that every such v can be written as

        (x,y,z)  =  c₁(0, 1, 1) + c₂(1, 0, 1) + c₃(1, 1, 0)

        =  (c₂ + c₃, c₁ + c₃, c₁ + c₂)

This corresponds to the system of equations

              c₂ + c₃  =  x
        c₁ +       c₃  =  y
        c₁ + c₂         =  z

which can be written in matrix form

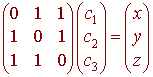
We can write this as 

        Ac  =  b

Notice that 

        det(A)  =  2

Hence A is nonsingular and

        c  =  A^-1b

So that a nontrivial solution exists.  To write (2,4,8) as a linear combination of vectors in S, we find that    

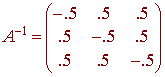
so that 

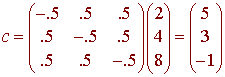
We have

        (2,4,8)  =  5(0,1,1) + 3(1,0,1) + (-1)(1,1,0)

Example

Show that if

        v₁  =  t + 2        and         v₂  =  t² + 1

and  S  =  {v₁, v₂}

then 

        S does not span P₂

Solution

A general element of P₂ is of the form 

        v   =  at² + bt + c

We set 

        v  =  c₁v₁ + c₂v₂ 

or

        at² + bt + c  =  c₁(t + 2) + c₂(t² + 1)  =  c₂t² + c₁t + c₁ + c₂ 

Equating coefficients gives

        a  =  c₂
         b  =  c₁
         c  =  c₁ + c₂ 

Notice that if 

        a  =  1        b  =  1        c  =  1

there is no solution to this.  Hence S does not span V.

Example

Let 

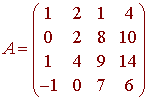
Find a spanning set for the null space of A.

Solution

We want the set of all vectors x with 

        Ax  =  0

We find that the rref of A is

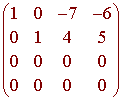
The parametric equations are

        x₁  =  7s + 6t
        x₂  =  -4s - 5t
        x₃  =  s
        x₄  =  t

We can get the span in the following way.  We first let

        s  =  1        and         t  =  0

to get 

        v₁  =  (7,-4,1,0)   

and let

        s  =  0        and     t  =  1

to get

        v₂  =  (6,-5,0,1)

If we let S  =  {v₁,v₂} then S spans the null space of A.

Linear Independence

We now know how to find out if a collection of vectors span a vector space.  It should be clear that if S  =  {v₁, v₂, ... , v_n) then Span(S) is spanned by S.  The question that we next ask is are there any redundancies.  That is, is there a smaller subset of S that also span Span(S).  If so, then one of the vectors can be written as a linear combination of the others. 

        v_i  =  c₁v₁ + c₂v₂ + ... + c_{i -1}v_{i -1} + c_i+1v_i+1 + ... + c_nv_n 

If this is the case then we call S a linearly dependent set.  Otherwise, we say that S is linearly independent.  There is another way of checking that a set of vectors are linearly dependent.  

Theorem

Let S  =  {v₁, v₂, ... , v_n) be a set of vectors, then S is linearly dependent if and only if 0 is a nontrivial linear combination of vectors in S.  That is, there are constants c₁, ..., c_n with at least one of the constants nonzero with

         c₁v₁ + c₂v₂ + ... + c_nv_n  =  0 

Proof

Suppose that S is linearly dependent, then

        v_i  =  c₁v₁ + c₂v₂ + ... + c_{i -1}v_{i -1} + c_i+1v_i+1 + ... + c_nv_n 

Subtracting v_i from both sides, we get

         c₁v₁ + c₂v₂ + ... + c_{i -1}v_{i -1} + v_i  + c_i+1v_i+1 + ... + c_nv_n  =  0

In the above equation c_i  =  1 which is nonzero, so that 0 is a nontrivial linear combination of vectors in S.  

Now let 

         c₁v₁ + c₂v₂ + ... + c_{i -1}v_{i -1} + c_iv_i  + c_i+1v_i+1 + ... + c_nv_n  =  0

with c_i nonzero.  Divide both sides of the equation by c_i and let a_j  =  -c_j / c_i to get

         -a₁v₁ - a₂v₂ - ... - a_{i -1}v_{i -1} + v_i - a_i+1v_i+1 - ... - a_nv_n  =  0

finally move all the terms to the other right side of the equation to get

        v_i  =  a₁v₁ + a₂v₂ + ... + a_{i -1}v_{i -1} + a_i+1v_i+1 + ... + a_nv_n 

Example

Show that the set of vectors 

        S  =  {(1, 1, 3, 4),  (0, 2, 3, 1),  (4, 0, 0, 2)}

are linearly independent.

Solution

We write

        c₁(1, 1, 3, 4) + c₂(0, 2, 3, 1) + c₃(4, 0, 0, 2)  =  0

We get four equations

        c₁ + 4c₃  =  0
        c₁ + 2c₂  =  0
        3c₁ + 3c₂  =  0
        4c₁ + c₂ + 2c₃  =  0

The matrix corresponding to this homogeneous system is 

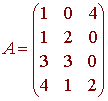
and

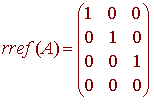
Hence 

        c₁  =  c₂  =  c₃  =  0

and we can conclude that the vectors are linearly independent.

Example

Let   

        S  =  {cos² t, sin² t, 4)

then S is a linearly dependent set of vectors since

        4  =  4cos²t + 4sin²t

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions