Vectors in Rn
Definition and Properties
We assume that you are already familiar with vectors in R2 and R3, so that you will see that the definition extends naturally.
A vector in Rn is a n x 1 matrix.
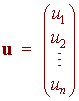
The set of all vectors in Rn is called n-space.
We define the sum and difference of two vectors and the product of a scalar and a vector by just realizing that vectors are matrices.
Example
Let
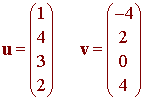 then
then
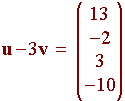
Properties of Vectors
Vectors enjoy the following properties.
If u, v, and w are vectors and c and d are scalars, then
- u
+ v = v + u
- u
+ (v + w) = (u + v) + w
- There
is a 0 with
u + 0 = 0 + u = u
for all vectors u.
- For
any u there
is a -u
with u + (-u)
= 0.
- cu
is a vector in Rn.
- c(u
+ v) = cu + cv
- (c
+ d)u = cu + du
- c(du)
= (cd)u
- 1u = u
The proofs of all of these come from the properties of real numbers since the definition of addition subtraction and scalar multiplication is given componentwise. For example to prove number 6, we have
[(c + d)u]i = (c + d)[u]i = c[u]i + d[u]i = [cu]i + [du]i
Dot Product and Length
Just as we defined the dot product for vectors in R2 and R3, we similarly define the dot product for two vectors in the more general Rn.
Let
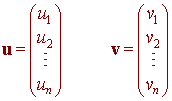
then the dot product (or scalar product) of u and v is defined by
u . v = S uivi
We define the length or magnitude of a vector as
![]()
A vector is a unit vector if it has length one. The unit vector in the direction of u is given by
u
||u||
and the distance between u and v by
Distance = ||u - v||
The angle q between two vectors is defined by
u . v
cos q
=
||u|| ||v||
u and v are orthogonal if
u . v = 0
Example
Let
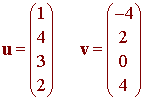
as in the first example, then
u . v = (1)(-4) + (4)(2) + (3)(0) + (2)(4) = 12
and the distance between u and v is
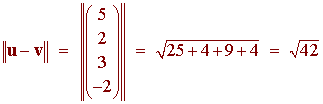
The unit vector in the direction of u is
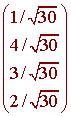
The angle between u and v is defined by
![]()
and
![]()
Properties of the Dot Product
Next we give some basic properties of the dot product.
Let u, v, and w be vectors and c be a scalar, then
- u
. u > 0;
u . u =
0 if and only if u
= 0.
- u
. v = v . u.
- (u
+ v) . w = u . w
+ v . w.
- (cu) . v = u . (cv) = c(u . v).
We will prove property 2 and leave the rest of the proofs for you.
Proof of 2
u . v = S uivi = S viui = v . u
Another important property called the Cauchy-Schwartz inequality is important enough to stand by itself.
Cauchy-Schwartz Inequality
If u and v are vectors then
|u . v| < ||u|| ||v||
If equality holds, we say that u and v are parallel. This will occur only if u is a multiple of v.
Proof
The proof is this is quite tricky. We let x be a scalar and note from property 1 that
0 < (xu + v) . (xu + v)
= u . u x2 + 2 u . v x + v . v
Since the dot product produces a scalar, the above equation is a quadratic in x. A quadratic that is always positive has nonpositive discriminant. Hence
(2 u . v)2 - 4(u . u)(v . v) < 0
dividing by 4 gives
(u . v)2 - (u . u)(v . v) < 0
or
(u . v)2 < (u . u)(v . v)
Taking the square root of both sides produces the result.
The final property of the dot product that we will discuss comes from geometry. We all know that the shortest distance between two points is a straight line. If we want to travel from the origin to a point P, it is quicker to go along the straight path then to go to a point Q first and then to P. If we choose the point P to be the tip of the vector u + v, and Q to be the tip of the vector u, then we have a following diagram.
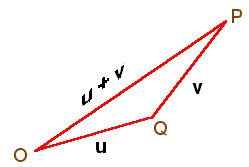
This leads us the the triangle inequality.
The Triangle Inequality
If u and v are vectors then
||u + v|| < ||u|| + ||v||
Proof
We take the square of the left hand side
||u + v||2 = (u + v) . (u + v) = u . u + 2 u . v + v . v
= ||u||2 + 2(u . v) + ||v||2 < ||u||2 + 2||u|| ||v|| + ||v||2 by Cauchy-Schwartz
= (||u|| + ||v||)2
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions