Subspaces

Definition and Examples

Definition

Let V be a vector space and let S be a subset of V such that S is a vector space with the same + and * from V.  Then S is called a subspace of V.

Remark:  Every vector space V contains at least two subspace, namely V and the set {0}.

Example

Let V be the vector space R³ and let S be the set of points that lie on the plane

        z  =  x - y

Then S is a subspace of V.

This is true since S is closed under + and *.  A point belonging to S has the form

        (x, y, x - y)

If 

        (x₁, y₁, x₁ - y₁)          and        (x₂, y₂, x₂ - y₂) 

are in S then

        (x₁, y₁, x₁ - y₁) + (x₂, y₂, x₂ - y₂)  =  (x₁ + x₂, y₁+ y₂, x₁ - y₁ + x₂ - y₂)

        =  (x₁ + x₂, y₁+ y₂, (x₁ + x₂) - (y₁ + y₂))

is in S.  We also have

        c(x₁, y₁, x₁ - y₁)  =  (cx₁, cy₁, cx₁ - cy₁)

is in S.  The rest of the properties follow immediately since they are true in V.  In fact, the two closure properties are all we need to show when we want to check that any subspace S is a subspace of any vector space V.

Theorem

Let V be a vector space and S be a subset of V.  If S is closed under + and * then S is a subspace of V.

The proof of this theorem only involves noticing that the properties are all true in S by virtue of being true in V.

Example

Set V be the vector space of all differentiable functions and let S be the subset of V such that for any f in V

        f '(0)  =  1

Then S is not a subspace of V since if f and g are in S, then 

        (f + g)'(0)  =  f '(0) + g'(0)  =  1 + 1  =  2

Hence S is not closed under +.

Example

Let S be the subset of M^2x2 of trace 0, that is the sum of the diagonal entries is zero.  Then S is a subspace of M^2x2.  Elements of S have the form

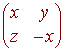
so if

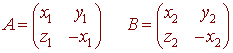
then

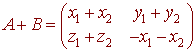
has zero trace.  And 

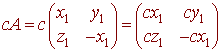
also has trace zero.  Hence S is closed under + and *.  We can conclude that S is a subspace of V.

The Range and Null Space of a Matrix

There are two subspaces that deserve special attention.  Recall that an m x n matrix A is associated with a linear transformation from Rⁿ  --->  R^m.  We defined subspaces of Rⁿ and R^m as follows.

Definition

Let A be an m by n matrix.  

Define the null space of A to be the subspace consisting of vectors x in Rⁿ with the property 

        Ax  =  0

and define the range of A to be the subspace consisting of vectors y in R^m such that there is a b in Rⁿ with

        Ab  =  y 

To prove that the null space and range are subspaces of Rⁿ and R^m respectively, we need to show that closure is satisfied.  We will show this for the null space and leave the range as an exercise.  Let u and v be elements of the null space.  Then

        A(u + v)  =  Au + Av  =  0 + 0  =  0

and

        A(cu)  =  cAu  =  c* 0  =  0 

hence the null space is a subspace of Rⁿ.

Linear Combinations and Span

Example

Suppose that V  =  P₂ and let

        f(t)  =  t² - t        and        g(t)  =  t + 1

Let S be the subset of P₂ that consists of all polynomials of the form 

        c₁f + c₂g

where c₁ and c₂ are constants.  Then S is called the span of f and g and is a subspace of P₂.  We will show closure under *.  Closure under + is also not difficult to show and is left to the reader to check.  Let

        u  =  c₁f + c₂g 

and c be a constant.  Then

        cu  =  cc₁f + cc₂g  =  af + bg

so is in S.

In general, if V is a vector space and S  =  {v₁,v₂, ...,v_n} is a subset of V, then we call

        c₁v₁ + c₂v₂ + ... + c_nv_n 

a linear combination of S.  The set of all linear combinations of S is called the span of S and is a subspace of V.

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions