Rank

Row Space

A common theme of matrices has been viewing a matrix as either a collection of row vectors or a collection of column vectors.  Let us first consider the matrix A as a collection of row vectors. 

Let

        S  =  {v₁,v₂,...,v_n}

where v_i is the i^th row of A and is a vector in Rⁿ.  Then the space spanned by {v₁,v₂,...,v_n} is called the row space of A.

Notice that the row operations will not change the row space of A.  (Convince yourself of this).  This gives us the following theorem

Theorem

If A and B are row equivalent matrices, then their row spaces are equal.

To find a basis for the row space of a matrix, we just find its rref.  The rows of the rref will form a basis of the row space.

Example

Find a basis for the row space of

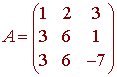
Solution

We find

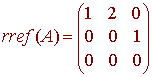
The first two rows

        {(1,2,0), (0,0,1)}

are a basis for the row space of A.

Notice that for any A, the nonzero rows of rref(A) will be linearly independent.  This is true since each nonzero row v_i contains a corner.  That is the k^th entry of this row is 1 while the rest of the rows have a 0 for the k^th entry.  In particular, the k^th entry of

        c₁v₁ + ... + c_rv_r

is equal to c_k.  Hence if the above expression is zero then all of the constants are zero and the vectors are linearly independent.

Of particular interest is the dimension of the row space.  We call the dimension of the row space of a matrix A the row rank of A.

In the above example the row rank of A is 2 since there are 2 vector in a basis for the row space of A.

The Column Space of a Matrix

We can also view a matrix as the collection of column vectors.

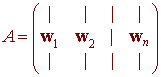
We can ask the corresponding question, "What is a basis for the space spanned by the column vectors {w₁,w₂, ... ,w_n}of A?"  We call this space the column space of A and its the dimension the column rank of A.

Example

Let

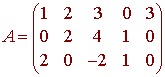
Find a basis for the column space of A consisting only of column vectors of A.  Then find a basis for the row space of A consisting only of rows of A.

Solution

We will use the following fact that we will not prove.  See your textbook for the proof.

Let A be a matrix and B be the rref of A.  Let 

        {w₁,w₂, ... , w_k}

be the columns of B that contain corners.  Then the corresponding columns of A are a basis for the column space of A.

We find the rref(A) to be

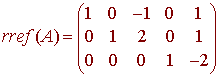
The first second and fourth columns of this matrix contain the corners. Hence the first second and fourth columns of A 

        (1,0,2), (2,2,0), (0,1,1)

form a basis for the column space of A.  The column rank is 3.

To find a basis for the row space of A consisting only of rows of A, we notice that the column space of A^T is the row space of A.  We have 

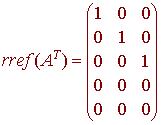
Hence the basis for the column space of A^T consists of the first three columns (all three columns)

        (1,0,-1,0,1), (0,1,2,0,1), (0,0,0,1,-2)

and these form a basis for the row space of A.

Notice that the column rank and the row rank are the same for the above matrix.  This will always be true since the number of vectors in each space corresponds to the number of corners of rref(A).

We call the column rank (which is equal to the row rank) the rank.

Related Theorems

The next thing to notice is that each column that does not contain a corner corresponds to a basis vector of the null space of A.  We call the dimension of the null space the nullity of A.  Putting this all together gives 

Theorem

Let A be an m x n matrix, then

        rank(A) + nullity(A)  =  n

If A is an n x n matrix then nullity(A)  =  0 if and only if rank(A)  =  n. In this case, the matrix is nonsingular.  Also the rank(A)  =  n if and only if the column rank of A  =  n if and only if the row rank of A  =  n.  We can now add three more items to our list of nonsingular equivalencies.  

Let A be an n x n matrix.  Then TFAE

1. A is nonsingular.
   
   
2. Ax  =  0  has only the trivial solution.
   
   
3. A is row equivalent to I.
   
   
4. Ax  =  b has a unique solution for all b. 
   
   
5. det(A) is nonzero.
   
   
6. A has rank n.
   
   
7. A has nullity 0.
   
   
8. The rows of A are linearly independent.
   
   
9. The columns of A are linearly independent.

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions