Orthogonal Complements

Definition of the Orthogonal Complement

Geometrically, we can understand that two lines can be perpendicular in R² and that a line and a plane can be perpendicular to each other in R³.  We now generalize this concept and ask given a vector subspace, what is the set of vectors that are orthogonal to all vectors in the subspace.

Definition

Let V be a vector space and W be a subspace of V.  Then the orthogonal complement of W in V is the set of vectors u such that u is orthogonal to all vectors in W.

Example

Let V  =  R²  and W be the subspace spanned by (1,2).  Then  is the set of vectors (a,b) with

        (a,b) ^. c(1,2)  =  0  

or

        ac + 2bc  =  0        a + 2b  =  0

This is a 1 dimensional vector space spanned by

        (-2,1)

In the example above the orthogonal complement was a subspace.  This will always be the case.

Theorem

Let W be a subspace of a vector space V.  Then the orthogonal complement of W is also a subspace of V.  Furthermore, the intersection of W and its orthogonal complement is just the zero vector.

Proof

Let u₁ and u₂ be vectors in the orthogonal complement of W and c be a constant.  Then 

1.  If w is in W, then

        (u₁ + u₂) ^. w  =  u₁^. w + u₂ ^. w  =  0

2.  If w is in W, then

        (cu₁) ^. w  =  c(u₁ ^. w)  =  c(0)  =  0

Now we prove that the intersection is zero.  If v is in the intersection then we think of v first as being in W and second as being in the orthogonal complement of W.  Hence 

        v ^. v  =  0

This implies that

        v  =  0

The next theorem states that if w₁, ... ,w_r is a basis for W and u₁, ... ,u_k is a basis for then 

        {w₁, ... ,w_r, u₁, ... ,u_k}

is a basis for Rⁿ.  In symbols, we write

Theorem

We leave it up to you to look up the proof of this statement.  What this means is that every vector v in Rⁿ can be uniquely written in the form

        v  =  w + u 

with w in W and u in .

A corollary of this theorem is the following

Corollary

First if a vector is in W then it is orthogonal to every vector in the orthogonal complement of W.  If a vector v is orthogonal to every vector in the orthogonal complement of W, and also by the theorem above we have 

        v  =  w + u

with w in W and u in the orthogonal complement of W.  Since u is in the orthogonal complement of W, we have 

        0  =  v ^. u  =  (w + u) ^. u  =  w ^. u + u ^. u  =  u ^. u

Hence u  =  0 and v  =  w.

Matrices and Complements

If we think of matrix multiplication as a collection of dot products then if

        Ax  =  0

then x is orthogonal to each of the rows of A.  Also if 

        A^Ty  =  0

then y is orthogonal to each of the columns of A.  More precisely we have 

Theorem

1.  The null space of A is the orthogonal complement of the row space of A.

2.  The null space of A^T is the orthogonal complement of the column space of A.

Example

Find a basis for the orthogonal complement of the space spanned by (1,0,1,0,2), (0,1,1,1,0) and (1,1,1,1,1).

Solution

We find the null space of the matrix

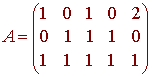
We find the rref of A.

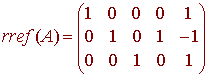
We get a basis 

        {(0,-1,0,1,0), (-1,1,-1,0,1)}

Projections

        Given a vector v and a subspace W with orthogonal basis w₁, ... , w_n, we are often interested in finding in finding the vector in W that is closest to v.  This closest vector is 

                             v ^. w₁               v ^. w₂                            v ^. w_n    
        proj_Wv  =                   w₁+                    w₂   + ... +                    w_n                          
                            w₁ ^. w₁               w₂ ^. w₂                                  w_n ^. w_n  

We will use this formula when we talk about inner product spaces and Fourier coefficients.  Notice that if W is orthonormal then the denominators are all equal to one.

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions