Homogeneous Systems
The Null Space
We have seen that the solution to the homogeneous system of equations
Ax = 0
is a subspace of Rn. We will now begin a discussion of how to find a basis for this system. The approach we will take is by an illustrative example.
Example
Find a basis for the null space of the matrix
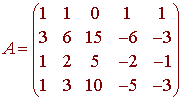
Solution
We have seen before that the null spaces of row equivalent matrices are the same. Hence this question is equivalent to that of finding the null space of
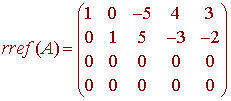
Now lets rewrite the system in equation form
x1 -5x3 + 4x4
+ 3x5 = 0
x2
+ 5x3 - 3x4 - 2x5 = 0
We can move the last three variable (the ones that are not corner variables) to the right hand side of the equations and add identity equations to get
x1 = 5x3 - 4x4 - 3x5
x2 = -5x3
+ 3x4 + 2x5
x3
= x3
x4
= x4
x5
= x5
It is useful to introduce parameters here
s1 = x3 s2 = x4 s3 = x5
so that
x1 = 5s1 - 4s2 - 3s3
x2 = -5s1
+ 3s2 + 2s3
x3
= s1
x4
=
s2
x5
=
s3
and we can write this in vector form
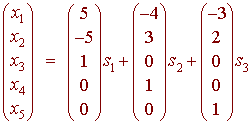
We can see that the null space is represented by triplets (s1, s2, s3). This is equivalent (isomorphic) to the space R3. We select the standard basis
(1,0,0), (0,1,0), (0,0,1)
and come up with the basis for the null space
{(5,-5,1,0,0), (-4,3,0,1,0), (-3,2,0,0,1)}
Example
Let
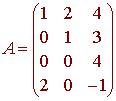
Find the null space of A.
Solution
As before, we find rref the matrix.
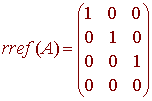
The corresponding equations are
x1 = 0
x2 = 0
x3 = 0
and we see that the null space is the subspace containing only 0.
Nonhomogeneous Systems
Now that we know how to solve the homogeneous equation
Ax = 0
we move on to nonhomogeneous systems
Ax = b
We use the technique of rref as with homogeneous systems. The next example illustrates.
Example
Solve
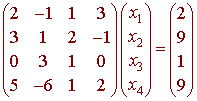
Solution
We solve the augmented matrix
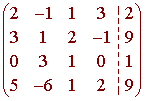
and find the rref of the augmented matrix. We get
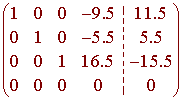
This gives us the solution
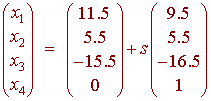
Notice that this is not a vector space (it does not contain the zero vector) so it does not make sense to ask for a basis for a null space.
The above answer shows that
The solution to
Ax = b
can be written in the form
x = xp + xh
Where
xp is a particular solution to the nonhomogeneous equation
xh represents the null space of A (the solution to the homogeneous equation)
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions