Computer Graphics
The Geometry of 2 x 2 Matrices
Since a 2 x 2 matrix corresponds uniquely to a linear transformation from R2 to R2, we can think of a matrix as transforming a planar figure into a new planar figure.
Example
Consider the matrix
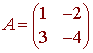
and the triangle with vertices (0,0), (12), (5,3). We have
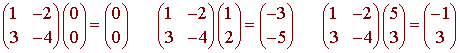
It is a property of linear transformations that if the matrix is nonsingular, then line segments map onto line segments. Hence triangles map onto triangles. The picture below shows the original triangle.
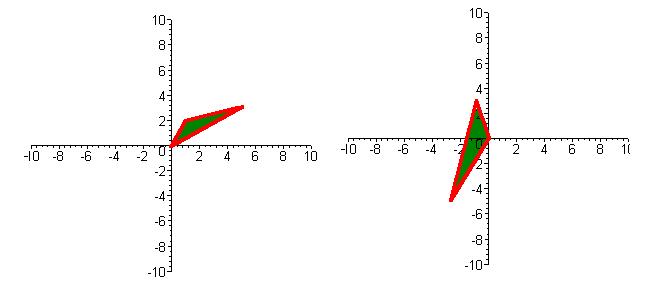
Some Basic Transformations
There are certain basic transformation that are building blocks for general transformations.
Example Reflection With Respect to the x axis.
To find the matrix for this transformation, we consider where the vectors e1 and e2 are mapped. The reflection with respect to the x-axis makes the y-coordinate negative and leaves the x-coordinate constant. We have
L(1, 0) = (1, 0) L(0, 1) = (0, -1)
These vectors are the column vectors for the matrix. We have
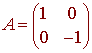
Example Reflection About the Line y = x
We see that
L(1,0) = (0,1) L(0,1) = (1,0)
so that
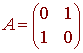
Example Rotation About an Angle q
The point (0,1) rotated about this angle is on the unit circle at radian angle q. The point (1,0) rotated about this angle is on the unit circle at radian angle p/2 + q. We have
L(1,0) = (cos q, sin q) L(0,1) = (cos(p/2 + q), sin(p/2 + q) = (-sin q, cos q)
We have
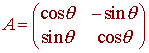
Example Shear in the y-direction
Another transformation that is common in computer graphics is a shear in the x or y direction. The picture below gives and example

The matrix that makes this happen is
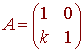
for some constant k.
You can find an interactive applets that lets you play with computer graphics and matrices at
http://www.ltcconline.net/greenl/java/Other/MatrixAnimation/MatrixAnimation.html
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions