Change of Basis
Coordinates
Consider the vector v = (2,5,3) in R3. In writing these coordinates we mean
v = 2e1 + 5e2 + 3e3
Where
e1 = (1,0,0) e2 = (0,1,0) e3 = (0,0,1)
are the standard basis vectors. Sometimes we are interested in finding the coordinates with respect to another basis.
Let S = {v1, v2, ... , vn} be a basis for a vector space V and let v be a vector in V and let
v = c1v1 + ... + cnvn
Then the coordinates of v with respect to the basis S is given by
[v]S = (c1, ... , cn)
Example
Consider the basis
S = {(1,2), (4,7)}
of R2 and let
v = (5,8)
presented in the standard basis. Find the coordinates of v in the basis S, that is find [v]S.
Solution
We set
(5,8) = c1(1,2) + c2(4,7)
or
c1
+ 4c2 = 5
2c1 + 7c2
= 8
We get the matrix equation
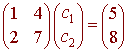
Notice that the matrix is just the matrix whose columns are the basis vectors of S. The solution to this is
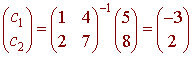
or
c1 = -3 c2 = 2
What we have seen here generalizes
Theorem
Let S = {v1, v2, ... , vn} be a basis for a vector space V and let v be a vector in V. Then
[v]S = A-1v
where A is the matrix whose column vectors are {v1, v2, ... , vn}
The proof involves going over the previous example and generalizing.
It is also interesting to run this process in reverse. Let S = {v1, v2, ... , vn}be a basis for V and let [v]S be given. We ask how to present v in the standard basis. This follows from the theorem. Since
[v]S = A-1v
We have
v = A[v]S
Example
Let
S = {(1,3,4), (2,-1,1), (1,0,2)}
be a basis for R3 and let
[v]S = (2,3,-1)
Find the coordinates with respect to the standard basis.
Solution
We just find
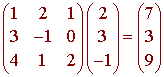
so that
v = (7,3,9)
Example
Let S = {(2,3), (1,4)} and T = {(0,2), (-1,5)} be two bases for R2, and let
[v]S = (-2,6)
Find [v]T
Solution
We can first find v in the standard basis. We have
v = AS[v]S
where AS is the matrix whose columns are the vectors in S. Now convert to the T basis.
[v]T = (AT)-1v = (AT)-1AS[v]S
or
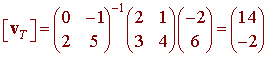
Example
Consider the vector v = 2 + 3t - t2 and let S = {t, t - 1, t2 - 1}. Find [v]S.
Solution
This problem looks a lot different from the previous ones, but looks can be deceiving. We notice that
t = 0(1) +
1(t) + 0(t2)
t - 1
= -1(1) + 1(t) + 0(t2)
t2 - 1
= -1(1) + 0(t) + 1(t2)
We write that
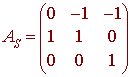
and use
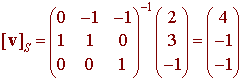
Transition Matrices
We have seen how to use the coordinates from one basis S into coordinates from another basis T. We have
[v]T = (AT)-1AS[v]S
The matrix given by
PT <-- S = (AT)-1AS
is called the transition matrix from the S basis to the T basis. Note that the transition matrix from the T basis to the S basis is given by
PS <-- T = (AS)-1AT = P-1T <-- S
Example
Find the transition matrix
PS <-- T
for the bases of M2x2 given by
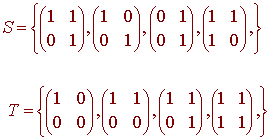
Then use this matrix to find [v]S
if
[v]T = (1,3,-2,4)
Solution
First we denote the standard basis by
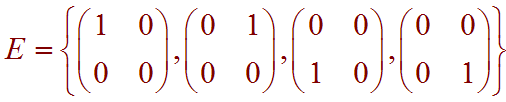
The AS is just the matrix of column vectors where each column is read as you would read the matrices in S. That is
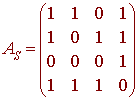
and similarly we have
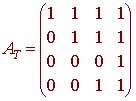
The transition matrix is
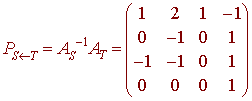
Now to find the coordinate in the S basis given T basis coordinates
[v]T = (1,3,-2,4)
we just multiply
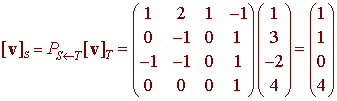
Remark: The transition matrix will always be nonsingular because of the nonsingular equivalence and that S and T are linearly independent.
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions