Basis and Dimension

Basis

In our previous discussion, we introduced the concepts of span and linear independence.  In a way a set of vectors S  =  {v₁, ... , v_k} span a vector space V if there are enough of the right vectors in S, while they are linearly independent if there are no redundancies.  We now combine the two concepts.

Definition of Basis

Let V be a vector space and S  =  {v₁, v₂, ... , v_k} be a subset of V.  Then S is a basis for V if the following two statements are true.

1. S spans V.
   
   
2. S is a linearly independent set of vectors in V.

Example

Let V  =  Rⁿ and let S  =  {e₁, e₂, ... ,e_n} where e_i has i^th component equal to 1 and the rest 0.  For example

        e₂  =  (0,1,0,0,...,0)

Then S is a basis for V called the standard basis.

Example

Let V  =  P₃ and let S  =  {1, t, t², t³}.  Show that S is a basis for V.

Solution

We must show both linear independence and span.  

Linear Independence:

Let 

        c₁(1) + c₂(t) + c₃(t²) + c₄(t³)  =  0

Then since a polynomial is zero if and only if its coefficients are all zero we have

        c₁  =  c₂  =  c₃  =  c₄  =  0

Hence S is a linearly independent set of vectors in V.

Span

A general vector in P₃ is given by 

        a + bt + ct² + dt³ 

We need to find constants c₁, c₂, c₃, c₄ such that 

        c₁(1) + c₂(t) + c₃(t²) + c₄(t³)  =  a + bt + ct² + dt³ 

We just let

                c₁  =  a,   c₂  =  b,   c₃  =  c,   c₄  =  d

Hence S spans V.  

We can conclude that S is a basis for V.

In general the basis {1, t, t², ... , tⁿ} is called the standard basis for P_n.  

Example

Show that S  =  {v₁, v₂, v₃, v₄} where

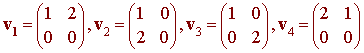
is a basis for V  =  M^2x2.  

Solution

We need to show that S spans V and is linearly independent.  

Linear Independence

We write

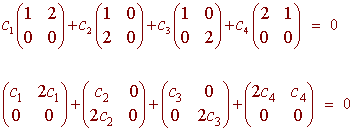
this gives the four equations

        c₁ + c₂ + c₃ + 2c₄  =  0
        2c₁              +   c₄  =  0
             2c₂                   =  0
                      2c₃          =  0

Which has the corresponding homogeneous matrix equation

        Ac  =  0

with

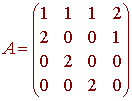
We have 

        det A  =  -12

Since the determinant is nonzero, we can conclude that only the trivial solution exists.  That is

        c₁  =  c₂  =  c₃  =  c₄  =  0

Span

We set

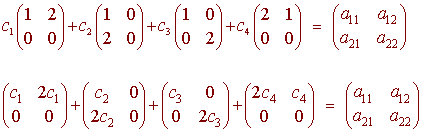
which gives the equations

        c₁ + c₂ + c₃ + 2c₄  =  x₁
        2c₁              +   c₄  =  x₂
             2c₂                   =  x₃
                      2c₃          =  x₄

The corresponding matrix equation is

        Ac  =  x

Since A is nonsingular, this has a unique solution, namely

        c  =  A^-1x

Hence S spans V.

We conclude that S is a basis for V.

If S spans V then we know that every vector in V can be written as a linear combination of vectors in S.  If S is a basis, even more is true.

Theorem

Let S  =  {v₁, v₂, ... , v_k} be a basis for V.  Then every vector in V can be written uniquely as a linear combination of vectors in S.

Remark:  What is new here is the word uniquely.

Proof

Suppose that 

        v  =  a₁v₁ + ... + a_nv_n  =  b₁v₁ + ... + b_nv_n 

then

        (a₁ - b₁)v₁ + ... + (a_n - b_n)v_n   =  0

Since S is a basis for V, it is linearly independent and the above equation implies that all the coefficients are zero.  That is

        a₁ - b₁  =  ... =  a_n - b_n  =  0

We can conclude that 

        a₁  =  b₁, ... , a_n  =  b_n 

Since linear independence is all about having no redundant vectors, it should be no surprise that if S = {v₁, v₂, ... , v_k}spans V, then if S is not linearly independent then we can remove the redundant vectors until we arrive at a basis.  That is if S is not linearly independent, then one of the vectors is a linear combination of the rest.  Without loss of generality, we can assume that this is the vector v_k.  We have that 

        v_k  =  a₁v₁ + ... + a_k-1v_k-1 

If v is any vector in S we can write 

        v  =  c₁v₁ + ... + c_kv_k  =  c₁v₁ + ... + c_k-1v_k-1 + c_k(a₁v₁ + ... + a_k-1v_k-1)

which is a linear combination of the smaller set 

        S' = {v₁, v₂, ... , v_k-1}

If S' is not a basis, as above we can get rid of another vector.  We can continue this process until the vectors are finally linear independent.  

We have proved the following theorem.

Theorem

Let S span a vector space V, then there is a subset of S that is a basis for V.

Dimension

We have seen that any vector space that contains at least two vectors contains infinitely many.  It is uninteresting to ask how many vectors there are in a vector space.  However there is still a way to measure the size of a vector space.  For example, R³ should be larger than R².  We call this size the dimension of the vector space and define it as the number of vectors that are needed to form a basis.  Tow show that the dimensions is well defined, we need the following theorem.

Theorem

If  S  =  {v₁, v₂, ... , v_n} is a basis for a vector space V and T = {w₁, w₂, ... , w_k} is a linearly independent set of vectors in V, then k < n.

Remark:  If S and T are both bases for V then k = n.  This says that every basis has the same number of vectors.  Hence the dimension is will defined.

The dimension of a vector space V is the number of vectors in a basis.  If there is no finite basis we call V an infinite dimensional vector space.  Otherwise, we call V a finite dimensional vector space.

Proof

If k > n, then we consider the set

        R₁  =  {w₁,v₁, v₂, ... , v_n}

Since S spans V, w₁ can be written as a linear combination of the v_i's.  

                w₁  =  c₁v₁ + ... + c_nv_n  

Since T is linearly independent, w₁ is nonzero and at least one of the coefficients c_i is nonzero.  Without loss of generality assume it is c₁.  We can solve for v₁ and write v₁ as a linear combination of w₁, v₂, ... v_n.  Hence 

        T₁  =  {w₁, v₂, ... , v_n}

is a basis for V.  Now let

        R₂  =  {w₁, w₂, v₂, ... , v_n}

Similarly, w₂ can be written as a linear combination of the rest and one of the coefficients is non zero.  Note that since w₁ and w₂ are linearly independent, at least one of the v_i coefficients must be nonzero.  We can assume that this nonzero coefficient is v₂ and as before we see that 

        T₂  =  {w₁, w₂,v_3, ... , v_n}

is a basis for V.  Continuing this process we see that 

        T_n  =  {w₁, w₂, ... , w_n}

Example

Since

        E  =  {e₁, e₂, ... , e_n}

is a basis for Rⁿ then dim Rⁿ  =  n.

Example

        dim P_n  =  n + 1

since 

        E  =  {1, t, t², ... , tⁿ} 

is a basis for P_n.

Example

        dim M^mxn  =  mn

We will leave it to you to find a basis containing mn vectors.

If we have a set of linearly independent vectors

        S  =  {v₁, v₂, ... , v_k}

with k < n, then S is not a basis.  From the definition of basis, S does not span V, hence there is a v_k+1 such that v_k+1 is not in the span of S.  Let 

        S₁  =  {v₁, v₂, ... ,v_k ,v_k+1}

S₁ is linearly independent.  We can continue this until we get a basis.

Theorem

Let 

        S  =  {v₁, v₂, ... , v_k}

be a linearly independent set of vectors in a vector space V.  Then there are vectors 

        v_k+1, ... , v_n 

such that 

        {v₁, v₂, ... , v_k, v_k+1, ... , v_n}

is a basis for V.

We finish this discussion with some very good news.  We have seen that to find out if a set is a basis for a vector space, we need to check for both linear independence and span.  We know that if there are not the right number of vectors in a set, then the set cannot form a basis.  If the number is the right number we have the following theorem.

Theorem

Let V be an n dimensional vector space and let S be a set with n vectors.  Then the following are equivalent.

1. S is a basis for V.
   
   
2. S is linearly independent.
   
   
3. S spans V.

Back to the Vectors Home Page

Back to the Linear Algebra Home Page

Back to the Math Department Home Page

e-mail Questions and Suggestions