Symmetric Matrices
In this discussion, we will look at symmetric matrices and see that diagonalizing is a pleasure. Recall that a matrix is symmetric if
A = AT
In other words the columns and rows of A are interchangeable. The next theorem we state without proof.
Theorem
Let A be a symmetric matrix and p(x) be the characteristic polynomial. Then all the roots of the characteristic polynomial p(x) are real. In particular the eigenvalues of A are real and there are n linearly independent eigenvectors and A is diagonalizable.
This says that a symmetric matrix with n linearly independent eigenvalues is always similar to a diagonal matrix. As good as this may sound, even better is true. First a definition.
A matrix P is called orthogonal if its columns form an orthonormal set and call a matrix A orthogonally diagonalizable if it can be diagonalized by D = P-1AP with P an orthogonal matrix.
Theorem
If A is an n x n symmetric matrix, then any two eigenvectors that come from distinct eigenvalues are orthogonal.
If we take each of the eigenvalues to be unit vectors, then the we have the following corollary.
Corollary
Symmetric matrices with n distinct eigenvalues are orthogonally diagonalizable.
Proof of the Theorem
We need to show that if v and w are eigenvectors corresponding to distinct real eigenvalues a and b, then v . w = 0. We have
a(v . w) = (av) . w = (Av) . w
= v . (ATw) = v . (Aw) = v . (bw)
= b(v . w)
Hence
(a - b)(v . w) = 0
since a and b are distinct, we can conclude that v and w are orthogonal.
We have used that
(Av) . w = v . (ATw)
a fact that is left for you as an exercise.
There is special property that holds for orthogonal matrices that is worth noting.
Theorem
Let P be an orthogonal matrix. Then
P-1 = PT
Proof
We need to show that if P is orthogonal, then
PTP = I
This follows immediately from the definition of orthogonal and matrix multiplication. If vj is the jth column of P, then
[PTP]ij = vi . vj
But since {v1, ..., vn} is an orthonormal set of vectors, we have
vi . vj = dij
The above theorem is especially useful, since computing a transpose is much easier than computing an inverse.
Example
Orthogonally diagonalize
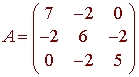
Solution
We find that the eigenvalues of A are 3, 6, and 9. To find the eigenvectors we find the null spaces.
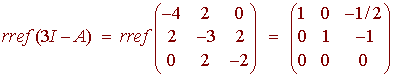
An eigenvector is (1/2, 1,1). We need to normalize this eigenvalue since it has magnitude 3/2. Dividing by the magnitude gives the unit vector (1/3, 2/3, 2/3). Next we have
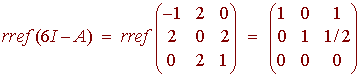
An eigenvector is (-1, -1/2,1). Again, we need to normalize this eigenvalue since it has magnitude 3/2. Dividing by the magnitude gives the unit vector (-2/3, -1/3, 2/3). Next we have
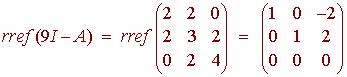
An eigenvector is (2, -2,1). Again, we need to normalize this eigenvalue since it has magnitude 3. Dividing by the magnitude gives the unit vector (2/3, -2/3, 1/3).
We now have
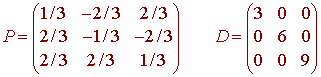
And we can write
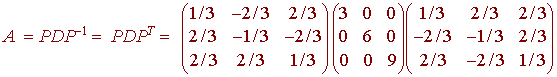
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions