The Matrix of a Linear Transformation
Finding the Matrix
We have seen how to find the matrix that changes from one basis to another. We have also seen how to find the matrix for a linear transformation from Rm to Rn. Now we will show how to find the matrix of a general linear transformation when the bases are given.
Let L be a linear transformation from V to W and let
S = {v1, ... ,vm} and T = {w1, ... ,wn}
be bases for V and W respectively. Then the matrix A representing L with respect to the bases S and T has ijth component that is the jth coordinate of the vector L(vi).
We start with the example when both bases are "standard". For this section, we will use the following conventions. We will use the letter "E" to denote the standard basis.
For Pn, we will call the basis
(Pn)E = {1, t, t2, ..., tn}
the "standard" basis.
For Mmxn, we will call the basis
MEmxn = {A11, A12, ..., A1n, A21, ..., A2n,... ..., Am1, ..., Amn}
the standard basis where Aij is the matrix with the ijth entry equal to 1 and all the rest are zero. With this convention, the standard basis for M3x2 is given by
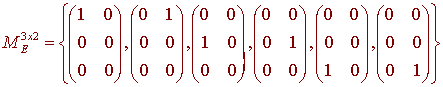
Example
Let L be the linear transformation from R2 to P2 defined by
L(x,y) = x + yt + (x + y)t2
Find the matrix representing L with respect to the standard bases.
Solution
Notice that
L(1,0) = 1 + t2 = (1,0,1) L(0,1) = t + t2 = (0,1,1)
hence the matrix is given by
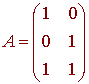
Now we will proceed with a more complicated example.
Example
Let L be the linear transformation from R2 to R2 such that
L(x,y) = (x - 2y, y - 2x)
and let
S = {(2, 3), (1, 2)}
be a basis for R2. Find the matrix for L that sends a vector from the S basis to the standard basis.
Solution
This involves two parts. The first is to find the matrix for L from the standard basis to the standard basis. This matrix is found by finding
L(1, 0) = (1, -2) and L(0,1) = (-2, 1)
The matrix is

Next we find the matrix from the S basis to the standard basis E. This matrix is
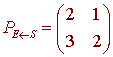
Now consider the diagram below
![]()
The matrix that we want is the composition of these two mappings. Remembering that composition of functions is written from right to left we get
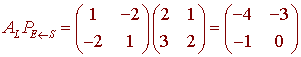
Example
Let L be the linear transformation from P2 to P2 with such that
L(a + bt + ct2) = (a + c) + (a + 2b)t + (a + b + 3c)t2
and let
S = {1 - t, 1 - t2, t - t2) and T = {2 + t + t2, 1 + t, 1 + t + t2}
Find the matrix of L with respect to the bases S and T.
Solution
We first find the matrix for L from the standard basis to the standard basis. We have
L(1,0,0) = L(1 + 0t + 0t2) = 1 + t + t2 = (1,1,1)
L(0,1,0) = L(0 + t + 0t2) = 2t + t2 = (0,2,1)
L(0,0,1) = L(0 + 0t + t2) = 1 + 3t2 = (1,0,3)
Hence the matrix for L with the standard bases is
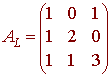
Next we find the transition matrices
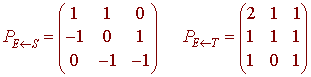
Now we consider the diagram below
![]()
Since matrices are functions, we compose the functions by multiplying the matrices from right to left. We get
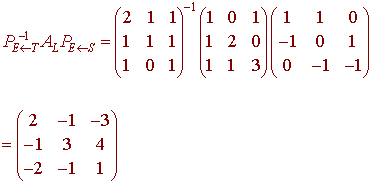
Example
Let L be the linear transformation from M2x2 to M2x2 and let
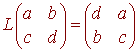
and
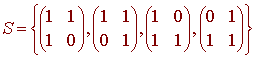
Find the matrix for L from S to S.
Solution
First we find the matrix for L in the standard basis. We have
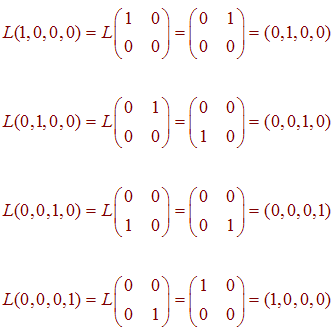
so that
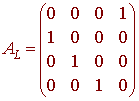
Next we have
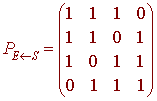
We use the diagram
![]()
and our matrix is
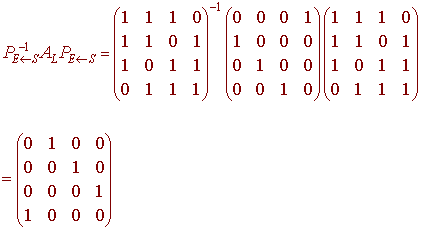
Diagonalizing
The last example showed us that the matrix for L was of the form
P-1AP
This was the definition of a matrix that is similar to A. If A is an n x n matrix and L is the linear transformation
L(v) = Av
and if the eigenvectors {v1, ... ,vn}are linearly independent then they form a basis for Rn. With
S = {v1, ... ,vn}
then we have seen that if P is the matrix whose ith column is vi, then
D = P-1AP
is a diagonal matrix. But this P is the transition matrix from the standard basis to the basis S. We have proven the following theorem.
Theorem
Let L be the linear transformation
L(v) = Av
then A is diagonalizable with n linearly independent eigenvectors S = {v1, ... ,vn} if and only if the matrix of L with respect to S is diagonal.
Orthogonal Matrices
We finish this discussion with a little geometry.
A linear transformation L called an isometry if for any u and v in V,
L(u) . L(v) = u . v
Notice that isometries preserve angles.
Theorem
L is an isometry if and only if the matrix of L with respect to the natural basis is orthogonal.
Proof
We use the fact that for any vectors x and y and matrix A,
(Ax) . y = x . (ATy)
If L is an isometry, then
u . v = L(u) . L(v) = Au . Av = u . (ATAv)
for all u and v. But then
v = ATAv
so that
ATA = I
that is, A is orthogonal
Conversely, if A is orthogonal, then
L(u) . L(v) = Au . Av = u . (ATAv) = u . v
so that L is an isometry.
Back to the Linear Algebra Home Page
Back to the Math Department Home Page
e-mail Questions and Suggestions